Skip to contents

K-Means Clustering with Lightweight Coreset

Source: R/clustering_kmeans18B.R
riem.kmeans18B.Rd

The modified version of lightweight coreset for scalable \(k\)-means computation is applied for manifold-valued data \(X_1,X_2,\ldots,X_N \in \mathcal{M}\). The smaller the set is, the faster the execution becomes with potentially larger quantization errors.

Usage

riem.kmeans18B(
  riemobj,
  k = 2,
  M = length(riemobj$data)/2,
  geometry = c("intrinsic", "extrinsic"),
  ...
)

Arguments

riemobj

a S3 "riemdata" class for \(N\) manifold-valued data.

k

the number of clusters.

M

the size of coreset (default: \(N/2\)).

geometry

(case-insensitive) name of geometry; either geodesic ("intrinsic") or embedded ("extrinsic") geometry.

...

extra parameters including

maxiter

maximum number of iterations to be run (default:50).

nstart

the number of random starts (default: 5).

Value

a named list containing

cluster

a length-\(N\) vector of class labels (from \(1:k\)).

means

a 3d array where each slice along 3rd dimension is a matrix representation of class mean.

score

within-cluster sum of squares (WCSS).

References

Bachem O, Lucic M, Krause A (2018). “Scalable k -Means Clustering via Lightweight Coresets.” In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery \& Data Mining, 1119--1127. ISBN 978-1-4503-5552-0.

See also

riem.coreset18B

Examples

#-------------------------------------------------------------------
#          Example on Sphere : a dataset with three types
#
# class 1 : 10 perturbed data points near (1,0,0) on S^2 in R^3
# class 2 : 10 perturbed data points near (0,1,0) on S^2 in R^3
# class 3 : 10 perturbed data points near (0,0,1) on S^2 in R^3
#-------------------------------------------------------------------
## GENERATE DATA
mydata = list()
for (i in 1:10){
  tgt = c(1, stats::rnorm(2, sd=0.1))
  mydata[[i]] = tgt/sqrt(sum(tgt^2))
}
for (i in 11:20){
  tgt = c(rnorm(1,sd=0.1),1,rnorm(1,sd=0.1))
  mydata[[i]] = tgt/sqrt(sum(tgt^2))
}
for (i in 21:30){
  tgt = c(stats::rnorm(2, sd=0.1), 1)
  mydata[[i]] = tgt/sqrt(sum(tgt^2))
}
myriem = wrap.sphere(mydata)
mylabs = rep(c(1,2,3), each=10)

## TRY DIFFERENT SIZES OF CORESET WITH K=4 FIXED
core1 = riem.kmeans18B(myriem, k=3, M=5)
core2 = riem.kmeans18B(myriem, k=3, M=10)
core3 = riem.kmeans18B(myriem, k=3, M=15)

## MDS FOR VISUALIZATION
mds2d = riem.mds(myriem, ndim=2)$embed

## VISUALIZE
opar <- par(no.readonly=TRUE)
par(mfrow=c(2,2), pty="s")
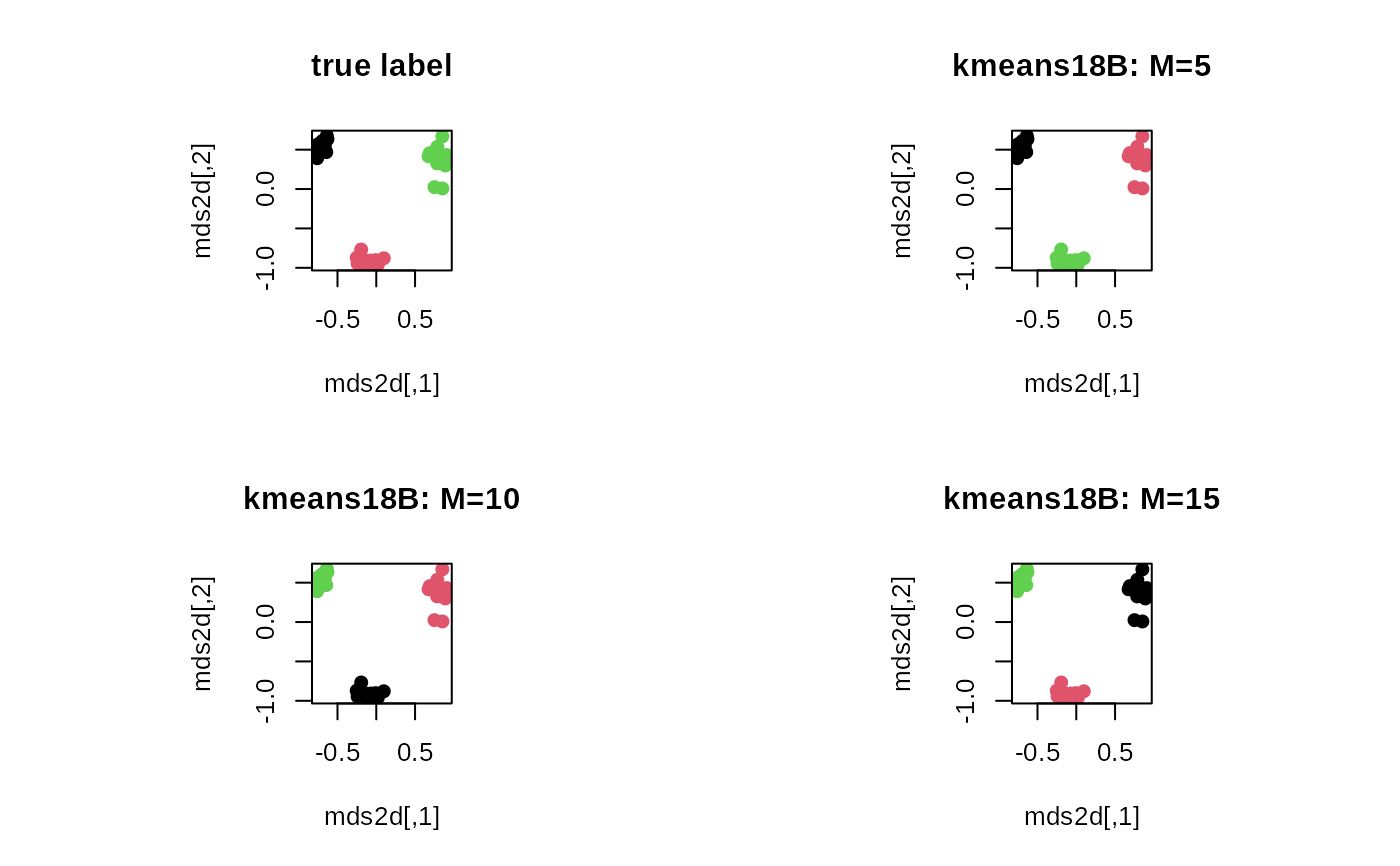
plot(mds2d, pch=19, main="true label", col=mylabs)
plot(mds2d, pch=19, main="kmeans18B: M=5",  col=core1$cluster)
plot(mds2d, pch=19, main="kmeans18B: M=10", col=core2$cluster)
plot(mds2d, pch=19, main="kmeans18B: M=15", col=core3$cluster)

par(opar)