Spherical Laplace Distribution

This is a collection of tools for learning with spherical Laplace (SL) distribution on a \((p-1)\)-dimensional sphere in \(\mathbf{R}^p\) including sampling, density evaluation, and maximum likelihood estimation of the parameters. The SL distribution is characterized by the following density function, $$f_{SL}(x; \mu, \sigma) = \frac{1}{C(\sigma)} \exp \left( -\frac{d(x,\mu)}{\sigma} \right)$$ for location and scale parameters \(\mu\) and \(\sigma\) respectively.

Usage

dsplaplace(data, mu, sigma, log = FALSE)

rsplaplace(n, mu, sigma)

mle.splaplace(data, method = c("DE", "Optimize", "Newton"), ...)

Arguments

data

data vectors in form of either an \((n\times p)\) matrix or a length-\(n\) list. See wrap.sphere for descriptions on supported input types.

mu

a length-\(p\) unit-norm vector of location.

sigma

a scale parameter that is positive.

log

a logical; TRUE to return log-density, FALSE for densities without logarithm applied.

n

the number of samples to be generated.

method

an algorithm name for concentration parameter estimation. It should be one of "Newton", "Optimize", and "DE" (case-sensitive).

...

extra parameters for computations, including

maxiter

maximum number of iterations to be run (default:50).

eps

tolerance level for stopping criterion (default: 1e-6).

use.exact

a logical to use exact (TRUE) or approximate (FALSE) updating rules (default: FALSE).

Value

dsplaplace gives a vector of evaluated densities given samples. rsplaplace generates unit-norm vectors in \(\mathbf{R}^p\) wrapped in a list. mle.splaplace computes MLEs and returns a list containing estimates of location (mu) and scale (sigma) parameters.

Examples

# \donttest{
# -------------------------------------------------------------------
#          Example with Spherical Laplace Distribution
#
# Given a fixed set of parameters, generate samples and acquire MLEs.
# Especially, we will see the evolution of estimation accuracy.
# -------------------------------------------------------------------
## DEFAULT PARAMETERS
true.mu  = c(1,0,0,0,0)
true.sig = 1

## GENERATE A RANDOM SAMPLE OF SIZE N=1000
big.data = rsplaplace(1000, true.mu, true.sig)

## ITERATE FROM 50 TO 1000 by 10
idseq = seq(from=50, to=1000, by=10)
nseq  = length(idseq)

hist.mu  = rep(0, nseq)
hist.sig = rep(0, nseq)

for (i in 1:nseq){
  small.data = big.data[1:idseq[i]]             # data subsetting
  small.MLE  = mle.splaplace(small.data)        # compute MLE
  
  hist.mu[i]  = acos(sum(small.MLE$mu*true.mu)) # difference in mu
  hist.sig[i] = small.MLE$sigma
}

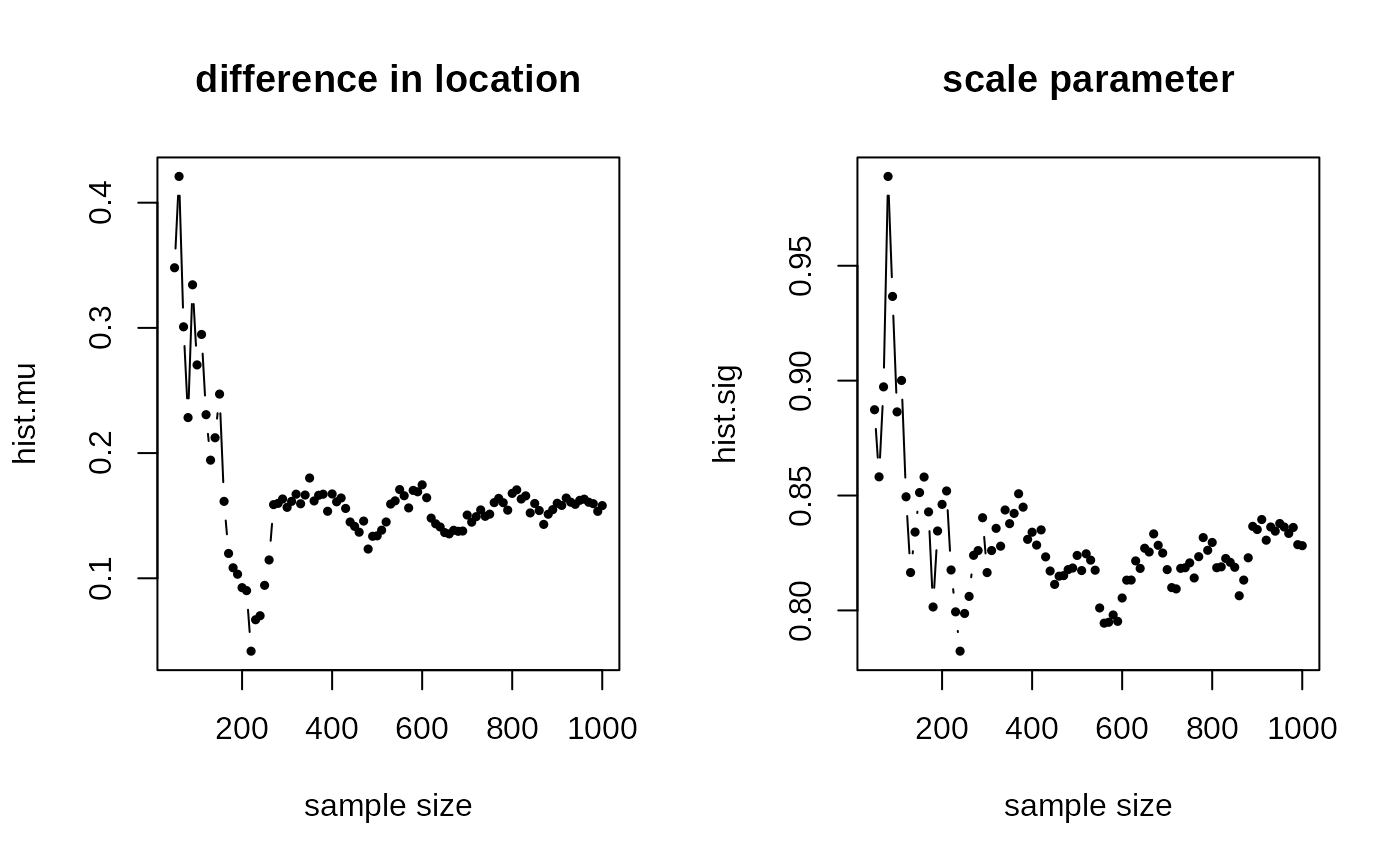
## VISUALIZE
opar <- par(no.readonly=TRUE)
par(mfrow=c(1,2))
plot(idseq, hist.mu,  "b", pch=19, cex=0.5, 
     main="difference in location", xlab="sample size")
plot(idseq, hist.sig, "b", pch=19, cex=0.5, 
     main="scale parameter", xlab="sample size")
abline(h=true.sig, lwd=2, col="red")

par(opar)
# }