Pairwise Distance on SPD Manifold

Given \(N\) observations \(X_1, X_2, \ldots, X_N\) in SPD manifold, compute pairwise distances among observations.

Usage

spd.pdist(spdobj, geometry, as.dist = FALSE)

Arguments

spdobj

a S3 "riemdata" class of SPD-valued data.

geometry

name of the geometry to be used. See spd.geometry for supported geometries.

as.dist

logical; if TRUE, it returns a dist object. Else, it returns a symmetric matrix.

Value

a S3 dist object or \((N\times N)\) symmetric matrix of pairwise distances according to as.dist parameter.

Examples

# \donttest{
#-------------------------------------------------------------------
#                   Two Types of Covariances
#
#  group1 : perturbed from data by N(0,1) in R^3
#  group2 : perturbed from data by [sin(x); cos(x); sin(x)*cos(x)]
#-------------------------------------------------------------------
## GENERATE DATA
spd_mats = array(0,c(3,3,20))
for (i in 1:10){
  spd_mats[,,i] = stats::cov(matrix(rnorm(50*3), ncol=3))
}
for (j in 11:20){
  randvec = stats::rnorm(50, sd=3)
  randmat = cbind(sin(randvec), cos(randvec), sin(randvec)*cos(randvec))
  spd_mats[,,j] = stats::cov(randmat + matrix(rnorm(50*3, sd=0.1), ncol=3))
}

## WRAP IT AS SPD OBJECT
spd_obj = wrap.spd(spd_mats)

## COMPUTE PAIRWISE DISTANCES
#  Geometries are case-insensitive.
pdA = spd.pdist(spd_obj, "airM")
pdL = spd.pdist(spd_obj, "lErm")
pdJ = spd.pdist(spd_obj, "Jeffrey")
pdS = spd.pdist(spd_obj, "stEin")
pdW = spd.pdist(spd_obj, "wasserstein")

## VISUALIZE
opar <- par(no.readonly=TRUE)
par(mfrow=c(2,3), pty="s")
image(pdA, axes=FALSE, main="AIRM")
image(pdL, axes=FALSE, main="LERM")
image(pdJ, axes=FALSE, main="Jeffrey")
image(pdS, axes=FALSE, main="Stein")
image(pdW, axes=FALSE, main="Wasserstein")
par(opar)

# }
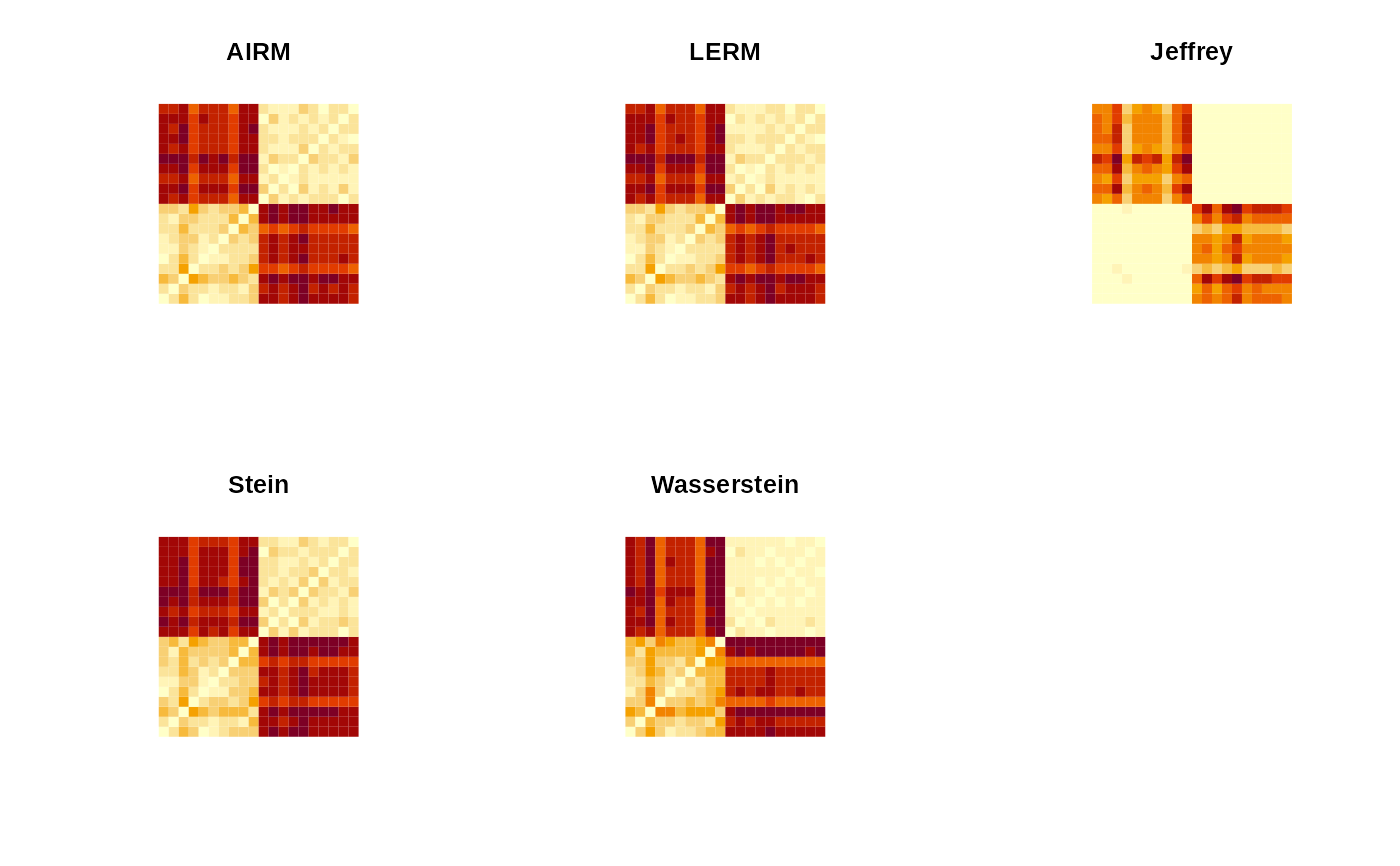