Wasserstein Distance between Empirical Measures

Given two empirical measures $\mu, \nu$ consisting of $M$ and $N$ observations, $p$-Wasserstein distance for $p\geq 1$ between two empirical measures is defined as $$\mathcal{W}_p (\mu, \nu) = \left( \inf_{\gamma \in \Gamma(\mu, \nu)} \int_{\mathcal{M}\times \mathcal{M}} d(x,y)^p d \gamma(x,y) \right)^{1/p}$$ where $\Gamma(\mu, \nu)$ denotes the collection of all measures/couplings on $\mathcal{M}\times \mathcal{M}$ whose marginals are $\mu$ and $\nu$ on the first and second factors, respectively.

Usage

riem.wasserstein(
  riemobj1,
  riemobj2,
  p = 2,
  geometry = c("intrinsic", "extrinsic"),
  ...
)

Arguments

riemobj1

a S3 "riemdata" class for $M$ manifold-valued data, which are atoms of $\mu$.

riemobj2

a S3 "riemdata" class for $N$ manifold-valued data, which are atoms of $\nu$.

p

an exponent for Wasserstein distance $\mathcal{W}_p$ (default: 2).

geometry

(case-insensitive) name of geometry; either geodesic ("intrinsic") or embedded ("extrinsic") geometry.

...

extra parameters including

weight1: a length-$M$ weight vector for $\mu$; if NULL (default), uniform weight is set.
weight2: a length-$N$ weight vector for $\nu$; if NULL (default), uniform weight is set.

Value

a named list containing

distance: $\mathcal{W_p}$ distance between two empirical measures.
plan: an $(M\times N)$ matrix whose rowSums and columnSums are weight1 and weight2 respectively.

Examples

#-------------------------------------------------------------------
#          Example on Sphere : a dataset with two types
#
# class 1 : 20 perturbed data points near (1,0,0) on S^2 in R^3
# class 2 : 30 perturbed data points near (0,1,0) on S^2 in R^3
#-------------------------------------------------------------------
## GENERATE DATA
mydata1 = list()
mydata2 = list()
for (i in 1:20){
  tgt = c(1, stats::rnorm(2, sd=0.1))
  mydata1[[i]] = tgt/sqrt(sum(tgt^2))
}
for (i in 1:30){
  tgt = c(rnorm(1,sd=0.1),1,rnorm(1,sd=0.1))
  mydata2[[i]] = tgt/sqrt(sum(tgt^2))
}
myriem1 = wrap.sphere(mydata1)
myriem2 = wrap.sphere(mydata2)

## COMPUTE p-WASSERSTEIN DISTANCES
dist1 = riem.wasserstein(myriem1, myriem2, p=1)
dist2 = riem.wasserstein(myriem1, myriem2, p=2)
dist5 = riem.wasserstein(myriem1, myriem2, p=5)

pm1 = paste0("p=1: dist=",round(dist1$distance,3))
pm2 = paste0("p=2: dist=",round(dist2$distance,3))
pm5 = paste0("p=5: dist=",round(dist5$distance,3))

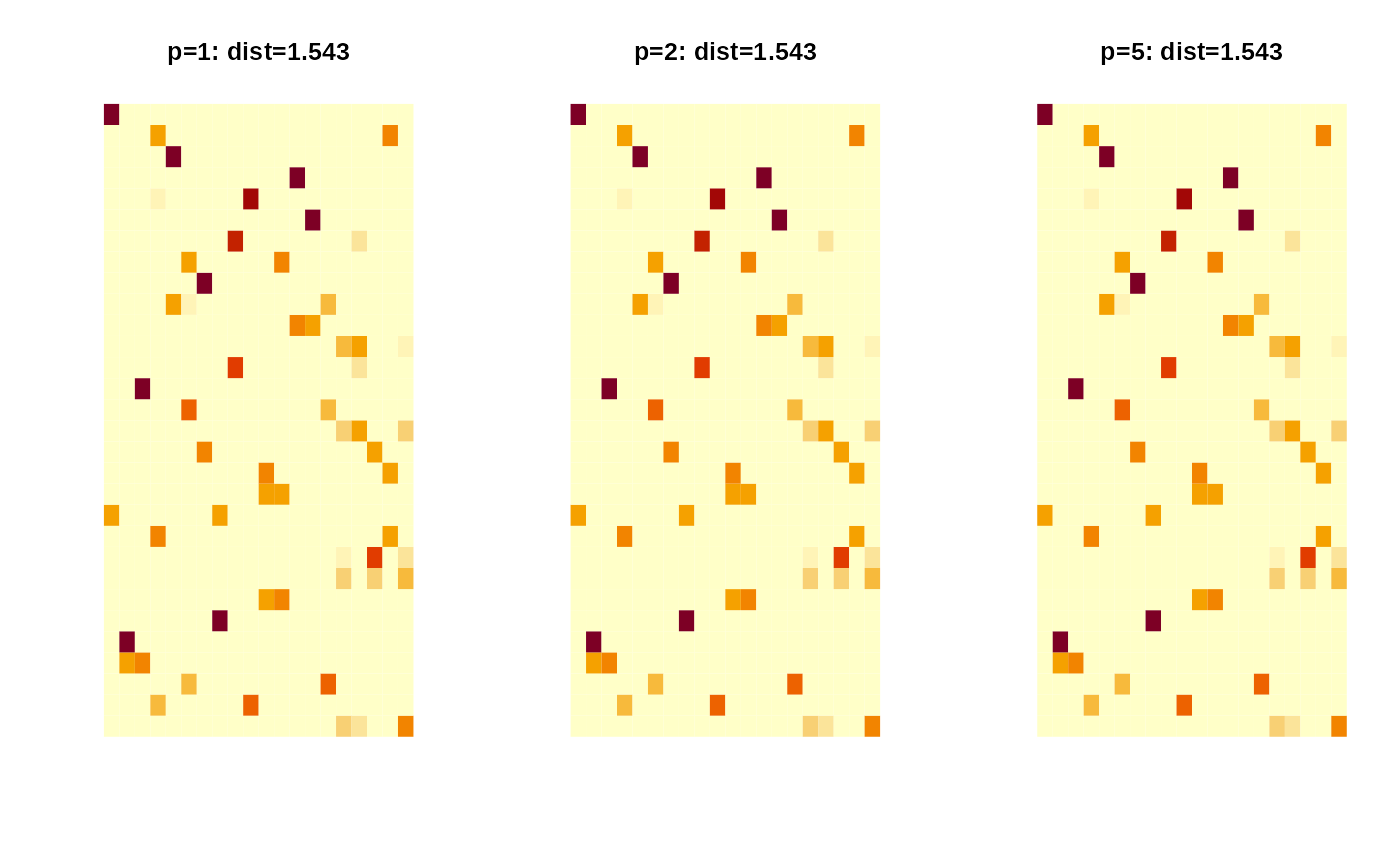
## VISUALIZE TRANSPORT PLAN AND DISTANCE
opar <- par(no.readonly=TRUE)
par(mfrow=c(1,3))
image(dist1$plan, axes=FALSE, main=pm1)
image(dist2$plan, axes=FALSE, main=pm2)
image(dist5$plan, axes=FALSE, main=pm5)

par(opar)