The version of Shi and Malik first constructs the affinity matrix $$A_{ij} = \exp(-d(x_i, d_j)^2 / \sigma^2)$$ where \(\sigma\) is a common bandwidth parameter and performs k-means clustering on the row-space of eigenvectors for the random-walk graph laplacian matrix $$L=D^{-1}(D-A)$$.
Usage
riem.scSM(riemobj, k = 2, sigma = 1, geometry = c("intrinsic", "extrinsic"))Arguments
- riemobj
a S3
"riemdata"class for \(N\) manifold-valued data.- k
the number of clusters (default: 2).
- sigma
bandwidth parameter (default: 1).
- geometry
(case-insensitive) name of geometry; either geodesic (
"intrinsic") or embedded ("extrinsic") geometry.
Value
a named list containing
- cluster
a length-\(N\) vector of class labels (from \(1:k\)).
- eigval
eigenvalues of the graph laplacian's spectral decomposition.
- embeds
an \((N\times k)\) low-dimensional embedding.
References
Shi J, Malik J (2000). “Normalized Cuts and Image Segmentation." IEEE Transactions on Pattern Analysis and Machine Intelligence, 22(8):888–905.
Examples
#-------------------------------------------------------------------
# Example on Sphere : a dataset with three types
#
# class 1 : 10 perturbed data points near (1,0,0) on S^2 in R^3
# class 2 : 10 perturbed data points near (0,1,0) on S^2 in R^3
# class 3 : 10 perturbed data points near (0,0,1) on S^2 in R^3
#-------------------------------------------------------------------
## GENERATE DATA
mydata = list()
for (i in 1:10){
tgt = c(1, stats::rnorm(2, sd=0.1))
mydata[[i]] = tgt/sqrt(sum(tgt^2))
}
for (i in 11:20){
tgt = c(rnorm(1,sd=0.1),1,rnorm(1,sd=0.1))
mydata[[i]] = tgt/sqrt(sum(tgt^2))
}
for (i in 21:30){
tgt = c(stats::rnorm(2, sd=0.1), 1)
mydata[[i]] = tgt/sqrt(sum(tgt^2))
}
myriem = wrap.sphere(mydata)
lab = rep(c(1,2,3), each=10)
## CLUSTERING WITH DIFFERENT K VALUES
cl2 = riem.scSM(myriem, k=2)$cluster
cl3 = riem.scSM(myriem, k=3)$cluster
cl4 = riem.scSM(myriem, k=4)$cluster
## MDS FOR VISUALIZATION
mds2d = riem.mds(myriem, ndim=2)$embed
## VISUALIZE
opar <- par(no.readonly=TRUE)
par(mfrow=c(1,4), pty="s")
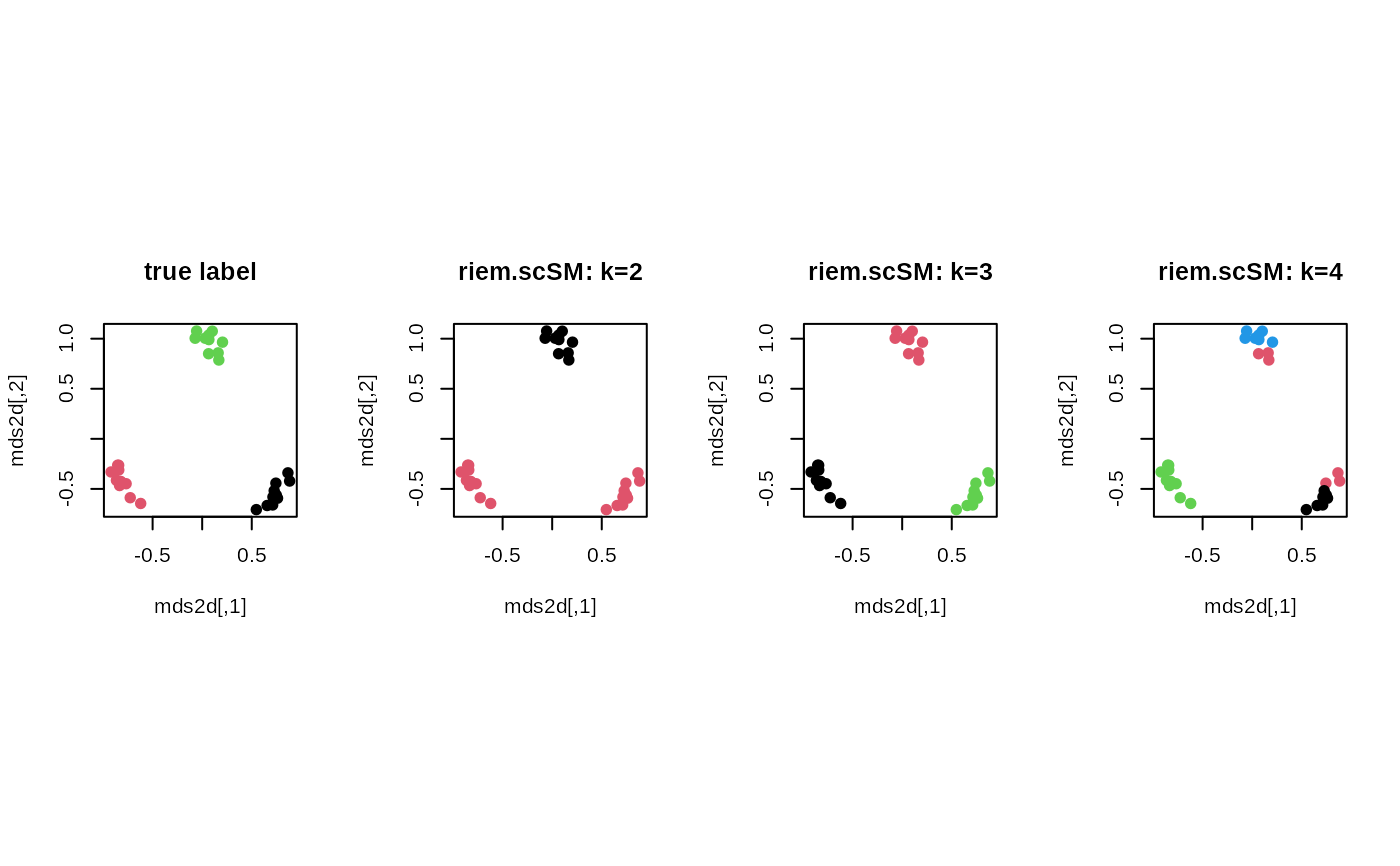
plot(mds2d, col=lab, pch=19, main="true label")
plot(mds2d, col=cl2, pch=19, main="riem.scSM: k=2")
plot(mds2d, col=cl3, pch=19, main="riem.scSM: k=3")
plot(mds2d, col=cl4, pch=19, main="riem.scSM: k=4")
 par(opar)
par(opar)
