Find K-Nearest Neighbors

Given \(N\) observations \(X_1, X_2, \ldots, X_N \in \mathcal{M}\), riem.knn constructs \(k\)-nearest neighbors.

Usage

riem.knn(riemobj, k = 2, geometry = c("intrinsic", "extrinsic"))

Arguments

riemobj

a S3 "riemdata" class for \(N\) manifold-valued data.

k

the number of neighbors to find.

geometry

(case-insensitive) name of geometry; either geodesic ("intrinsic") or embedded ("extrinsic") geometry.

Value

a named list containing

nn.idx

an \((N \times k)\) neighborhood index matrix.

nn.dists

an \((N\times k)\) distances from a point to its neighbors.

Examples

#-------------------------------------------------------------------
#          Example on Sphere : a dataset with three types
#
# * 10 perturbed data points near (1,0,0) on S^2 in R^3
# * 10 perturbed data points near (0,1,0) on S^2 in R^3
# * 10 perturbed data points near (0,0,1) on S^2 in R^3
#-------------------------------------------------------------------
## GENERATE DATA
mydata = list()
for (i in 1:10){
  tgt = c(1, stats::rnorm(2, sd=0.1))
  mydata[[i]] = tgt/sqrt(sum(tgt^2))
}
for (i in 11:20){
  tgt = c(rnorm(1,sd=0.1),1,rnorm(1,sd=0.1))
  mydata[[i]] = tgt/sqrt(sum(tgt^2))
}
for (i in 21:30){
  tgt = c(stats::rnorm(2, sd=0.1), 1)
  mydata[[i]] = tgt/sqrt(sum(tgt^2))
}
myriem = wrap.sphere(mydata)
mylabs = rep(c(2,3,4), each=10)

## K-NN CONSTRUCTION WITH K=5 & K=10
knn1 = riem.knn(myriem, k=5)
knn2 = riem.knn(myriem, k=10)

## MDS FOR VISUALIZATION
embed2 = riem.mds(myriem, ndim=2)$embed

## VISUALIZE
opar <- par(no.readonly=TRUE)
par(mfrow=c(1,2), pty="s")
plot(embed2, pch=19, main="knn with k=4", col=mylabs)
for (i in 1:30){
  for (j in 1:5){
    lines(embed2[c(i,knn1$nn.idx[i,j]),])
  }
}
plot(embed2, pch=19, main="knn with k=8", col=mylabs)
for (i in 1:30){
  for (j in 1:10){
    lines(embed2[c(i,knn2$nn.idx[i,j]),])
  }
}

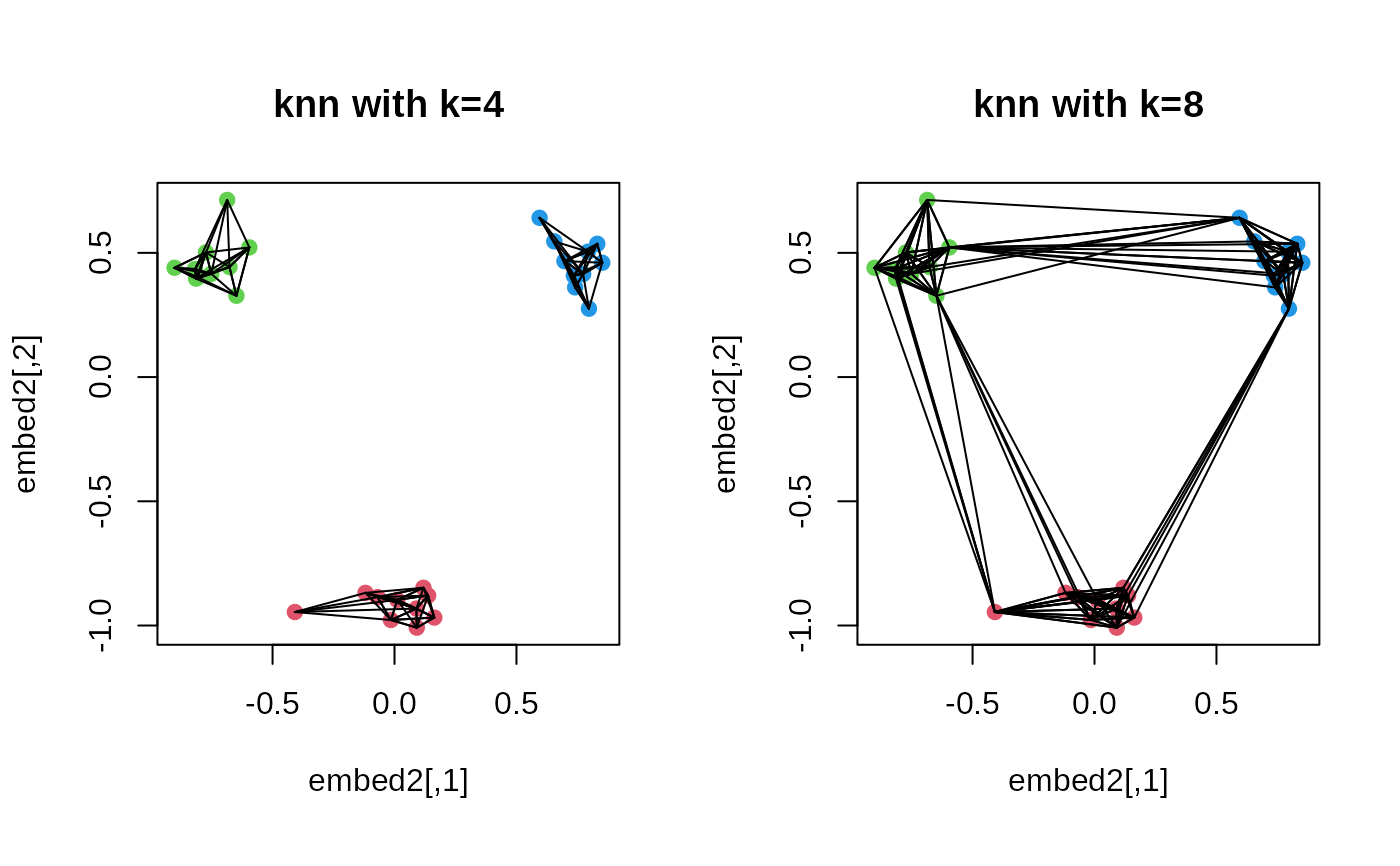par(opar)