Given 2 observations \(X_1, X_2 \in \mathcal{M}\), find the interpolated points of a geodesic \(\gamma(t)\) for \(t \in (0,1)\) which assumes two endpoints \(\gamma(0)=X_1\) and \(\gamma(1)=X_2\).
Arguments
- riemobj
a S3
"riemdata"class for \(2\) manifold-valued data where the first object is the starting point.- vect
a length-\(T\) vector in \((0,1)\) for which the interpolations are taken.
- geometry
(case-insensitive) name of geometry; either geodesic (
"intrinsic") or embedded ("extrinsic") geometry.
Value
a 3d array where \(T\) slices along 3rd dimension are interpolated objects in matrix representation.
Examples
#-------------------------------------------------------------------
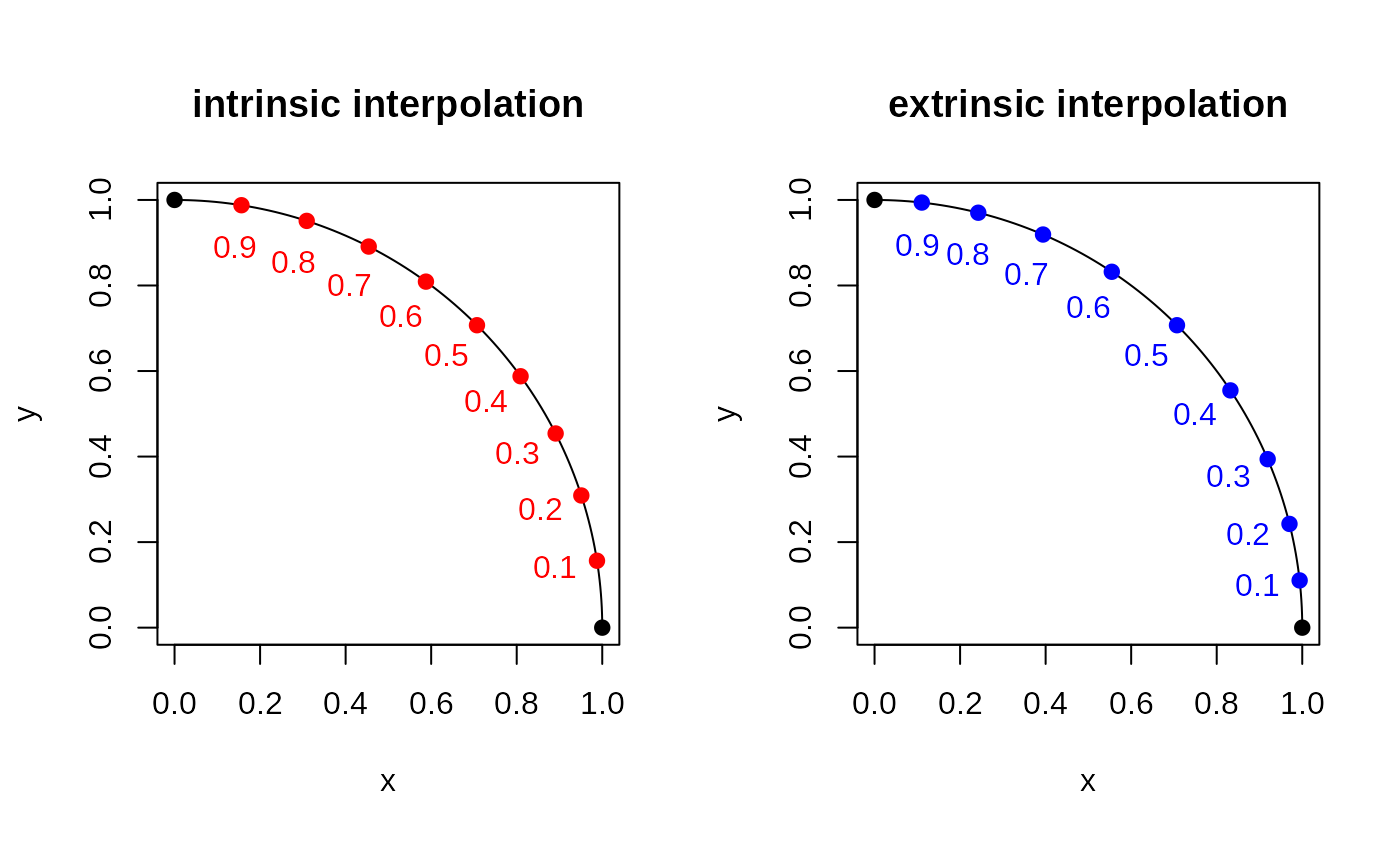
# Geodesic Interpolation between (1,0) and (0,1) in S^1
#-------------------------------------------------------------------
## PREPARE DATA
sp.start = c(1,0)
sp.end = c(0,1)
sp.data = wrap.sphere(rbind(sp.start, sp.end))
## FIND THE INTERPOLATED POINT AT FOR t=0.1, 0.2, ..., 0.9.
myvect = seq(from=0.1, to=0.9, by=0.1)
geo.int = riem.interps(sp.data, vect=myvect, geometry="intrinsic")
geo.ext = riem.interps(sp.data, vect=myvect, geometry="extrinsic")
geo.int = matrix(geo.int, byrow=TRUE, ncol=2) # re-arrange for plotting
geo.ext = matrix(geo.ext, byrow=TRUE, ncol=2)
## VISUALIZE
# Prepare Lines and Points
thetas = seq(from=0, to=pi/2, length.out=100)
quarter = cbind(cos(thetas), sin(thetas))
pts.int = rbind(sp.start, geo.int, sp.end)
pts.ext = rbind(sp.start, geo.ext, sp.end)
col.int = c("black", rep("red",9), "black")
col.ext = c("black", rep("blue",9), "black")
# Draw
opar <- par(no.readonly=TRUE)
par(mfrow=c(1,2), pty="s")
plot(quarter, main="intrinsic interpolation", # intrinsic geodesic
xlab="x", ylab="y", type="l")
points(pts.int, col=col.int, pch=19)
for (i in 1:9){
text(geo.int[i,1]*0.9, geo.int[i,2]*0.9,
paste0(round(i/10,2)), col="red")
}
plot(quarter, main="extrinsic interpolation", # intrinsic geodesic
xlab="x", ylab="y", type="l")
points(pts.ext, col=col.ext, pch=19)
for (i in 1:9){
text(geo.ext[i,1]*0.9, geo.ext[i,2]*0.9,
paste0(round(i/10,2)), col="blue")
}
par(opar)