Estimation of Distribution Algorithm with MACG Distribution

For a function \(f : Gr(k,p) \rightarrow \mathbf{R}\), find the minimizer and the attained minimum value with estimation of distribution algorithm using MACG distribution.

Usage

grassmann.optmacg(func, p, k, ...)

Arguments

func

a function to be minimized.

p

dimension parameter as in \(Gr(k,p)\).

k

dimension parameter as in \(Gr(k,p)\).

...

extra parameters including

n.start

number of runs; algorithm is executed n.start times (default: 10).

maxiter

maximum number of iterations for each run (default: 100).

popsize

the number of samples generated at each step for stochastic search (default: 100).

ratio

ratio in \((0,1)\) where top ratio*popsize samples are chosen for parameter update (default: 0.25).

print.progress

a logical; if TRUE, it prints each iteration (default: FALSE).

Value

a named list containing:

cost

minimized function value.

solution

a \((p\times k)\) matrix that attains the cost.

Examples

#-------------------------------------------------------------------
#               Optimization for Eigen-Decomposition
#
# Given (5x5) covariance matrix S, eigendecomposition is can be 
# considered as an optimization on Grassmann manifold. Here, 
# we are trying to find top 3 eigenvalues and compare.
#-------------------------------------------------------------------
# \donttest{
## PREPARE
A = cov(matrix(rnorm(100*5), ncol=5)) # define covariance
myfunc <- function(p){                # cost function to minimize
  return(sum(-diag(t(p)%*%A%*%p)))
} 

## SOLVE THE OPTIMIZATION PROBLEM
Aout = grassmann.optmacg(myfunc, p=5, k=3, popsize=100, n.start=30)

## COMPUTE EIGENVALUES
#  1. USE SOLUTIONS TO THE ABOVE OPTIMIZATION 
abase   = Aout$solution
eig3sol = sort(diag(t(abase)%*%A%*%abase), decreasing=TRUE)

#  2. USE BASIC 'EIGEN' FUNCTION
eig3dec = sort(eigen(A)$values, decreasing=TRUE)[1:3]

## VISUALIZE
opar <- par(no.readonly=TRUE)
yran = c(min(min(eig3sol),min(eig3dec))*0.95,
         max(max(eig3sol),max(eig3dec))*1.05)
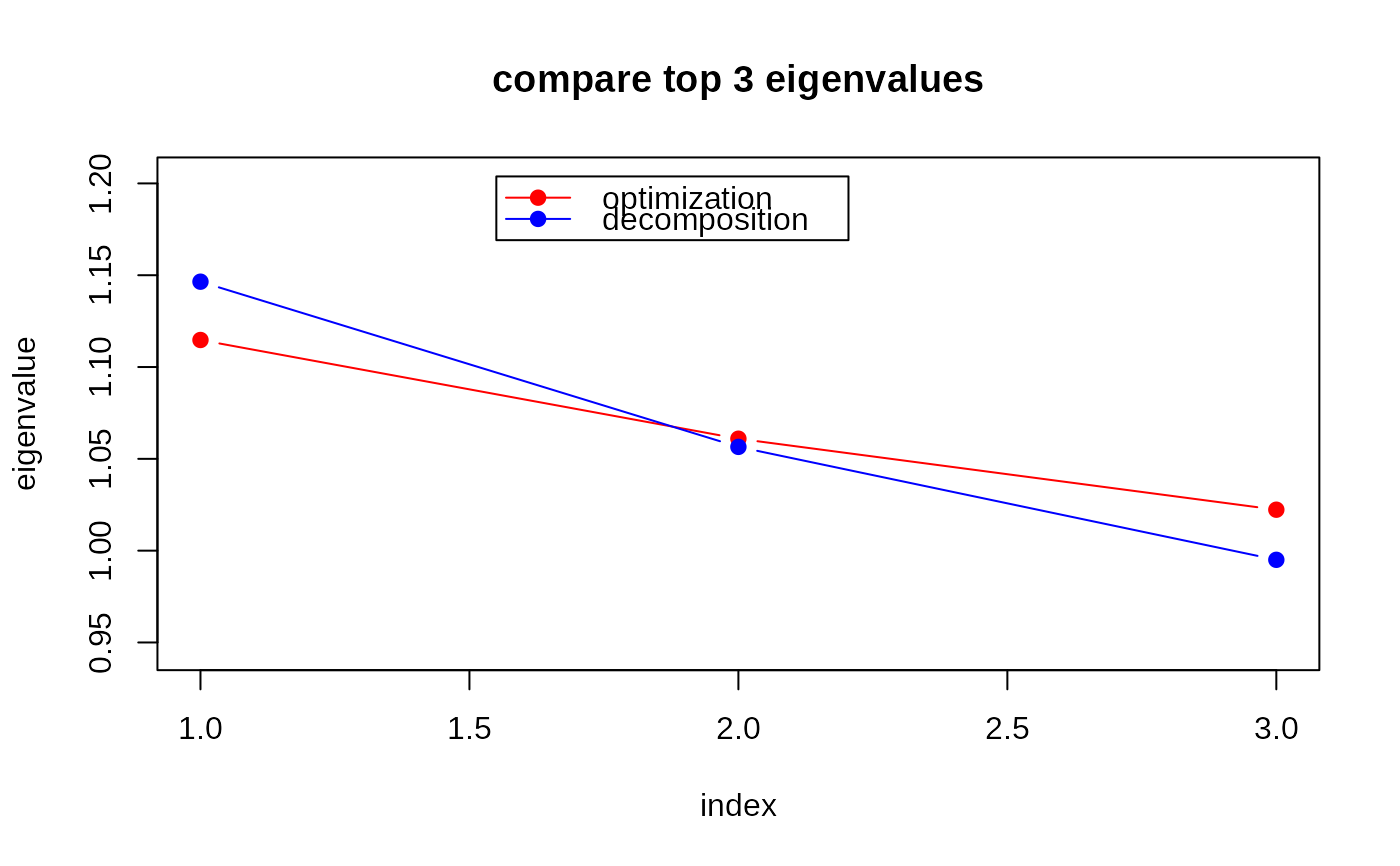
plot(1:3, eig3sol, type="b", col="red",  pch=19, ylim=yran,
     xlab="index", ylab="eigenvalue", main="compare top 3 eigenvalues")
lines(1:3, eig3dec, type="b", col="blue", pch=19)
legend(1.55, max(yran), legend=c("optimization","decomposition"), col=c("red","blue"),
       lty=rep(1,2), pch=19)

par(opar)
# }