Adaptive Dimension Reduction (Ding et al. 2002) iteratively finds the best subspace to perform data clustering. It can be regarded as one of remedies for clustering in high dimensional space. Eigenvectors of a between-cluster scatter matrix are used as basis of projection.
do.adr(X, ndim = 2, ...)Arguments
- X
an (n×p) matrix or data frame whose rows are observations.
- ndim
an integer-valued target dimension.
- ...
extra parameters including
- maxiter
maximum number of iterations (default: 100).
- abstol
absolute tolerance stopping criterion (default: 1e-8).
Value
a named Rdimtools S3 object containing
- Y
an (n×ndim) matrix whose rows are embedded observations.
- projection
a (p×ndim) whose columns are basis for projection.
- trfinfo
a list containing information for out-of-sample prediction.
- algorithm
name of the algorithm.
References
Ding C, Xiaofeng He, Hongyuan Zha, Simon HD (2002). “Adaptive Dimension Reduction for Clustering High Dimensional Data.” In Proceedings 2002 IEEE International Conference on Data Mining, 147--154.
See also
Examples
# \donttest{
## load iris data
data(iris)
set.seed(100)
subid = sample(1:150,50)
X = as.matrix(iris[subid,1:4])
label = as.factor(iris[subid,5])
## compare ADR with other methods
outADR = do.adr(X)
outPCA = do.pca(X)
outLDA = do.lda(X, label)
## visualize
opar <- par(no.readonly=TRUE)
par(mfrow=c(1,3))
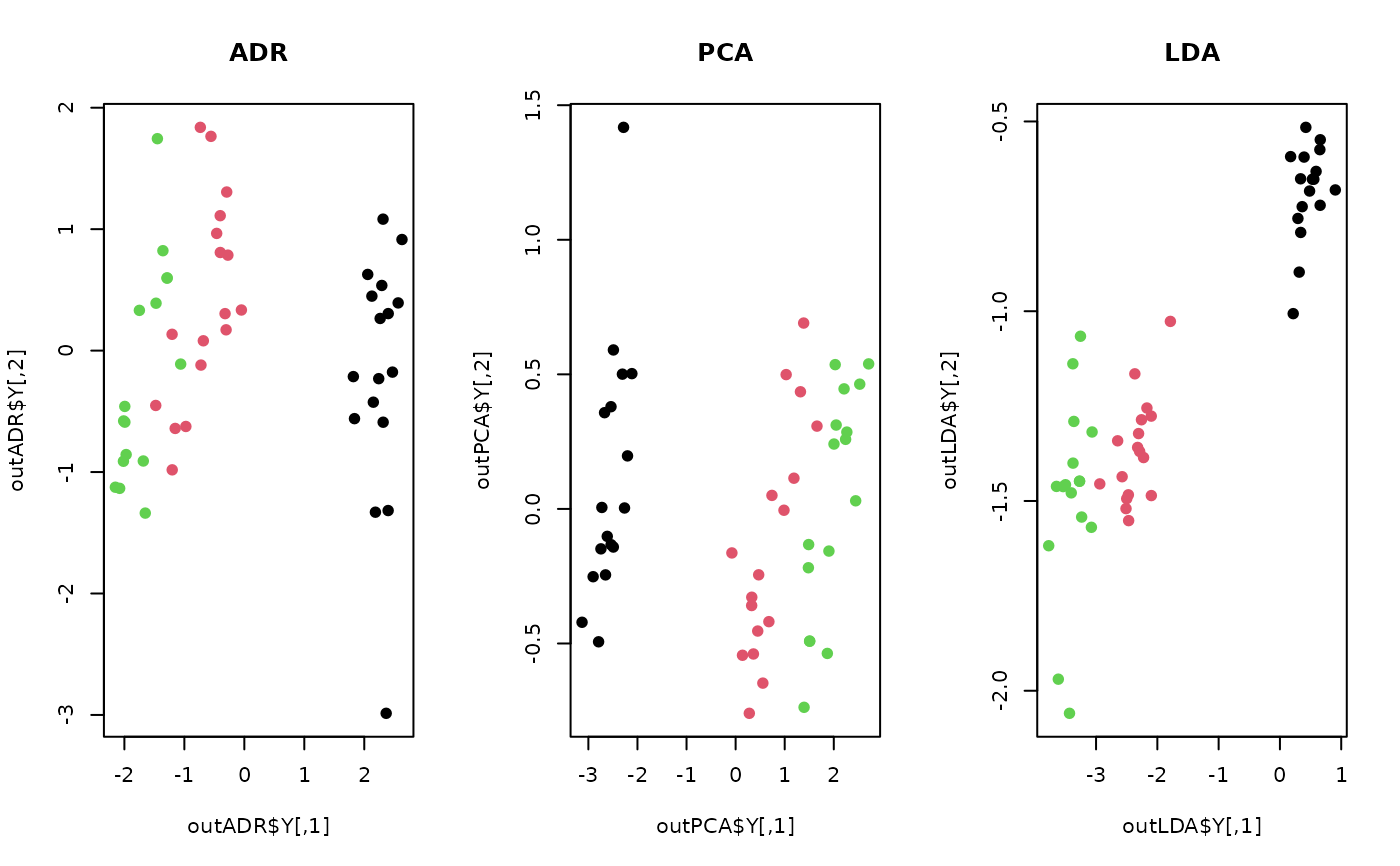
plot(outADR$Y, col=label, pch=19, main="ADR")
plot(outPCA$Y, col=label, pch=19, main="PCA")
plot(outLDA$Y, col=label, pch=19, main="LDA")
 par(opar)
# }
par(opar)
# }