Ruan et al. (2011) proposed a regularized covariance estimation by graphical lasso to cope with high-dimensional scenario where conventional GMM might incur singular covariance components. Authors proposed to use \(\lambda\) as a regularization parameter as normally used in sparse covariance/precision estimation problems and suggested to use the model with the smallest BIC values.
gmm11R(data, k = 2, lambda = 1, ...)
Arguments
| data | an \((n\times p)\) matrix of row-stacked observations. |
|---|---|
| k | the number of clusters (default: 2). |
| lambda | regularization parameter for graphical lasso (default: 1). |
| ... | extra parameters including
|
Value
a named list of S3 class T4cluster containing
- cluster
a length-\(n\) vector of class labels (from \(1:k\)).
- mean
a \((k\times p)\) matrix where each row is a class mean.
- variance
a \((p\times p\times k)\) array where each slice is a class covariance.
- weight
a length-\(k\) vector of class weights that sum to 1.
- loglkd
log-likelihood of the data for the fitted model.
- algorithm
name of the algorithm.
References
Ruan L, Yuan M, Zou H (2011). “Regularized Parameter Estimation in High-Dimensional Gaussian Mixture Models.” Neural Computation, 23(6), 1605--1622. ISSN 0899-7667, 1530-888X.
Examples
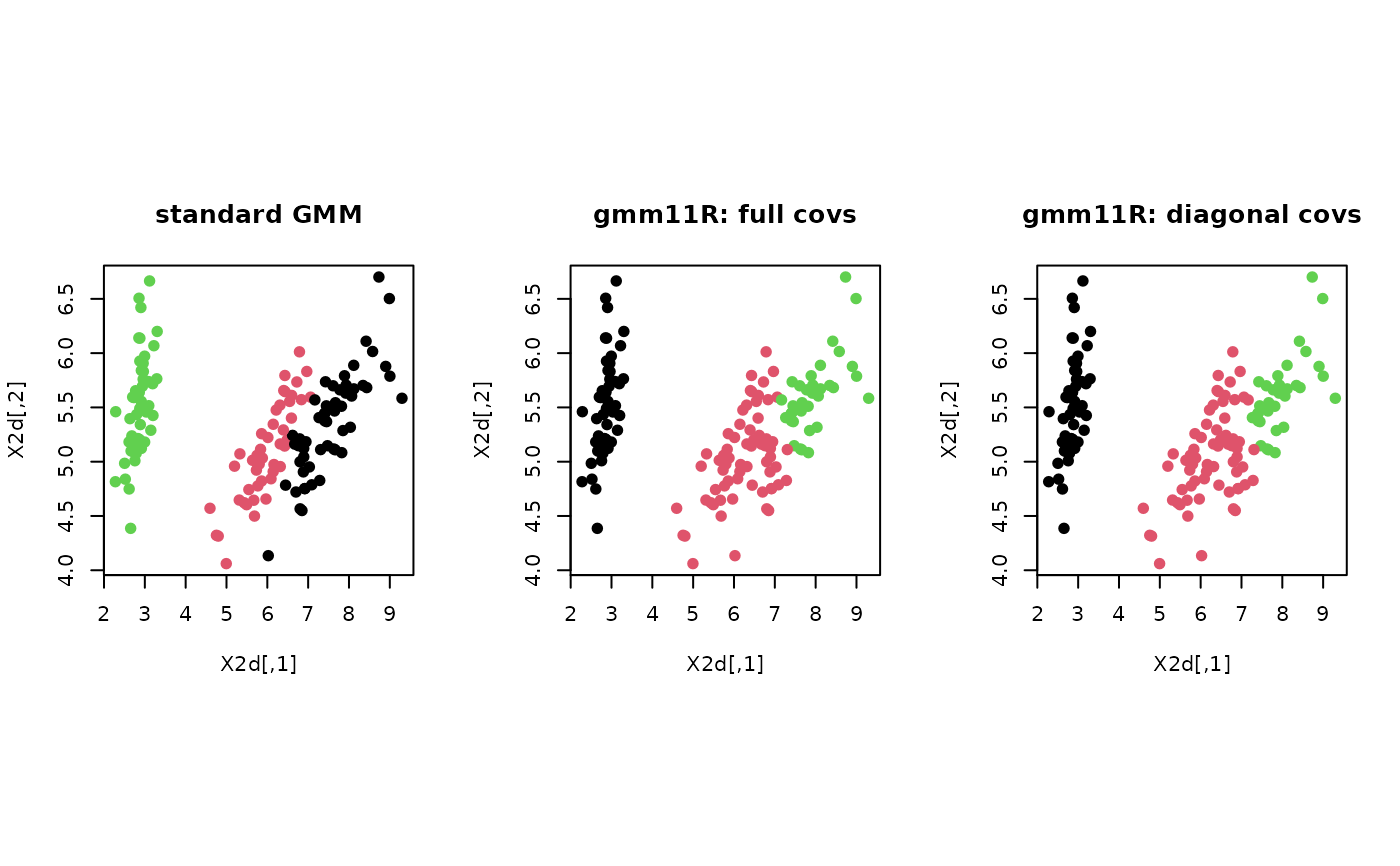
# ------------------------------------------------------------- # clustering with 'iris' dataset # ------------------------------------------------------------- ## PREPARE data(iris) X = as.matrix(iris[,1:4]) lab = as.integer(as.factor(iris[,5])) ## EMBEDDING WITH PCA X2d = Rdimtools::do.pca(X, ndim=2)$Y ## COMPARE WITH STANDARD GMM cl.gmm = gmm(X, k=3)$cluster cl.11Rf = gmm11R(X, k=3)$cluster cl.11Rd = gmm11R(X, k=3, usediag=TRUE)$cluster ## VISUALIZATION opar <- par(no.readonly=TRUE) par(mfrow=c(1,3), pty="s") plot(X2d, col=cl.gmm, pch=19, main="standard GMM") plot(X2d, col=cl.11Rf, pch=19, main="gmm11R: full covs") plot(X2d, col=cl.11Rd, pch=19, main="gmm11R: diagonal covs")