Orthogonal LDA (OLDA) is an extension of classical LDA where the discriminant vectors are orthogonal to each other.
do.olda(
X,
label,
ndim = 2,
preprocess = c("center", "scale", "cscale", "whiten", "decorrelate")
)Arguments
- X
an \((n\times p)\) matrix or data frame whose rows are observations and columns represent independent variables.
- label
a length-\(n\) vector of data class labels.
- ndim
an integer-valued target dimension.
- preprocess
an additional option for preprocessing the data. Default is "center". See also
aux.preprocessfor more details.
Value
a named list containing
- Y
an \((n\times ndim)\) matrix whose rows are embedded observations.
- trfinfo
a list containing information for out-of-sample prediction.
- projection
a \((p\times ndim)\) whose columns are basis for projection.
References
Ye J (2005). “Characterization of a Family of Algorithms for Generalized Discriminant Analysis on Undersampled Problems.” J. Mach. Learn. Res., 6, 483--502. ISSN 1532-4435.
Examples
## use iris data
data(iris)
set.seed(100)
subid = sample(1:150, 50)
X = as.matrix(iris[subid,1:4])
label = as.factor(iris[subid,5])
## compare with LDA
out1 = do.lda(X, label)
out2 = do.olda(X, label)
## visualize
opar <- par(no.readonly=TRUE)
par(mfrow=c(1,2))
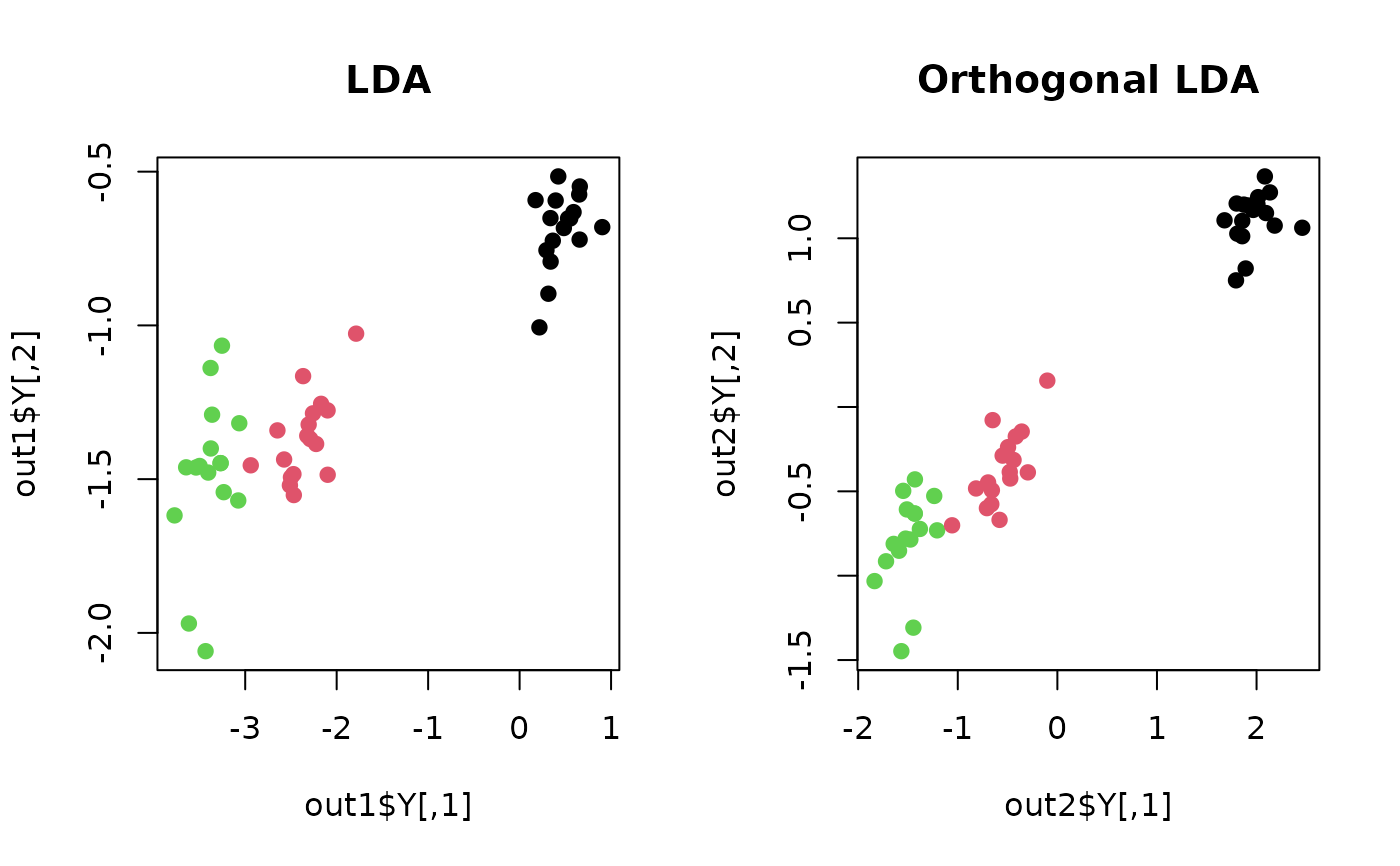
plot(out1$Y, pch=19, col=label, main="LDA")
plot(out2$Y, pch=19, col=label, main="Orthogonal LDA")
 par(opar)
par(opar)