Maximum Variance Projection (MVP) is a supervised method based on linear discriminant analysis (LDA). In addition to classical LDA, it further aims at preserving local information by capturing the local geometry of the manifold via the following proximity coding, $$S_{ij} = 1\quad\textrm{if}\quad C_i \ne C_j\quad\textrm{and} = 0 \quad\textrm{otherwise}$$, where \(C_i\) is the label of an \(i\)-th data point.
do.mvp(X, label, ndim = 2)Arguments
- X
an \((n\times p)\) matrix or data frame whose rows are observations and columns represent independent variables.
- label
a length-\(n\) vector of data class labels.
- ndim
an integer-valued target dimension.
Value
a named Rdimtools S3 object containing
- Y
an \((n\times ndim)\) matrix whose rows are embedded observations.
- projection
a \((p\times ndim)\) whose columns are basis for projection.
- algorithm
name of the algorithm.
References
Zhang T (2007). “Maximum Variance Projections for Face Recognition.” Optical Engineering, 46(6), 067206.
Examples
# \donttest{
## use iris data
data(iris)
set.seed(100)
subid = sample(1:150, 50)
X = as.matrix(iris[subid,1:4])
label = as.factor(iris[subid,5])
## perform MVP and compare with others
outMVP = do.mvp(X, label)
outPCA = do.pca(X)
outLDA = do.lda(X, label)
## visualize
opar <- par(no.readonly=TRUE)
par(mfrow=c(1,3))
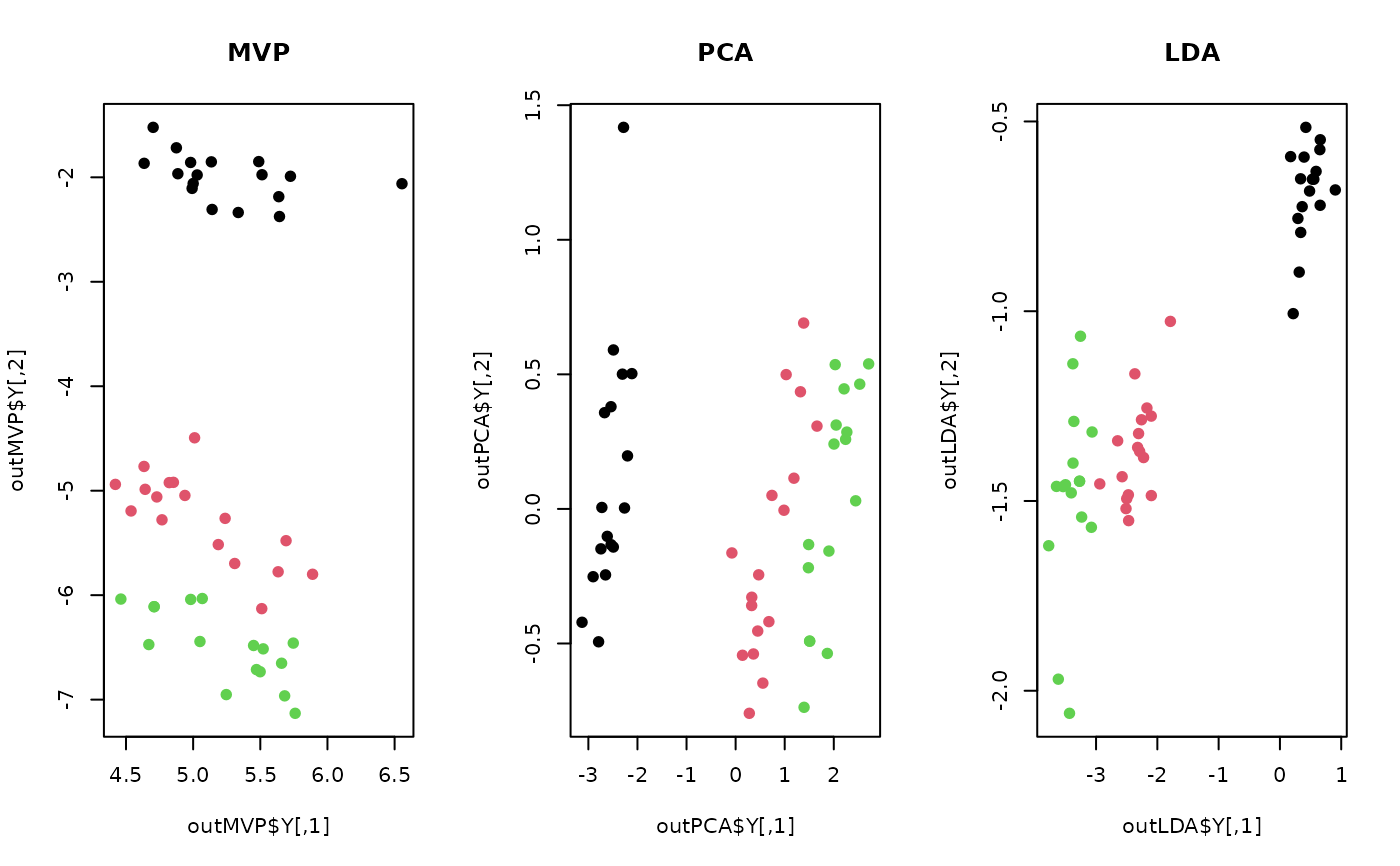
plot(outMVP$Y, col=label, pch=19, main="MVP")
plot(outPCA$Y, col=label, pch=19, main="PCA")
plot(outLDA$Y, col=label, pch=19, main="LDA")
 par(opar)
# }
par(opar)
# }