Local Similarity Preserving Projection

Local Similarity Preserving Projection (LSPP) is a variant of LPP in that it employs a sample-dependent graph generation process as of do.sdlpp. LSPP takes advantage of labeling information to correct local similarity weight in order to make intra-class weight larger than inter-class weight. It uses PCA preprocessing as suggested from the original work.

do.lspp(
  X,
  label,
  ndim = 2,
  t = 1,
  preprocess = c("center", "scale", "cscale", "decorrelate", "whiten")
)

Arguments

X: an \((n\times p)\) matrix or data frame whose rows are observations.
label: a length-\(n\) vector of data class labels.
ndim: an integer-valued target dimension.
t: kernel bandwidth in \((0,\infty)\).
preprocess: an additional option for preprocessing the data. Default is "center". See also aux.preprocess for more details.

Value

a named list containing

Y: an \((n\times ndim)\) matrix whose rows are embedded observations.
trfinfo: a list containing information for out-of-sample prediction.
projection: a \((p\times ndim)\) whose columns are basis for projection.

References

Huang P, Gao G (2015). “Local Similarity Preserving Projections for Face Recognition.” AEU - International Journal of Electronics and Communications, 69(11), 1724--1732.

Author

Kisung You

Examples

## generate data of 2 types with clear difference
diff = 15
dt1  = aux.gensamples(n=50)-diff;
dt2  = aux.gensamples(n=50)+diff;

## merge the data and create a label correspondingly
Y      = rbind(dt1,dt2)
label  = rep(1:2, each=50)

## compare with PCA
out1 <- do.pca(Y, ndim=2)
out2 <- do.slpp(Y, label, ndim=2)

## visualize
opar <- par(no.readonly=TRUE)
par(mfrow=c(1,2))
plot(out1$Y, col=label, pch=19, main="PCA")
plot(out2$Y, col=label, pch=19, main="LSPP")

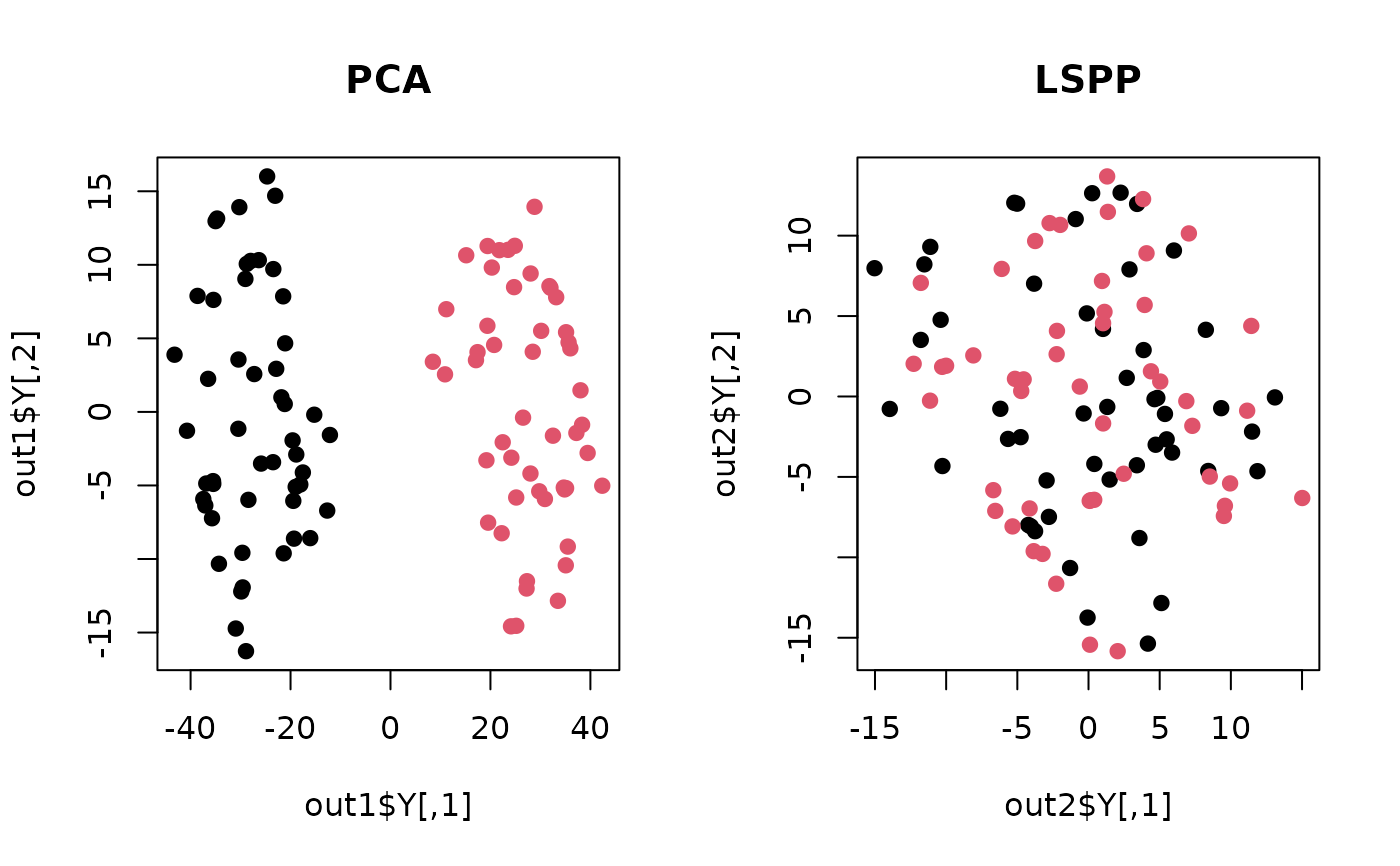par(opar)