Adaptive Maximum Margin Criterion (AMMC) is a supervised linear dimension reduction method.
The method uses different weights to characterize the different contributions of the
training samples embedded in MMC framework. With the choice of a=0, b=0, and
lambda=1, it is identical to standard MMC method.
do.ammc(
X,
label,
ndim = 2,
preprocess = c("center", "scale", "cscale", "decorrelate", "whiten"),
a = 1,
b = 1,
lambda = 1
)Arguments
- X
an \((n\times p)\) matrix or data frame whose rows are observations and columns represent independent variables.
- label
a length-\(n\) vector of data class labels.
- ndim
an integer-valued target dimension.
- preprocess
an additional option for preprocessing the data. Default is "center". See also
aux.preprocessfor more details.- a
tuning parameter for between-class weight in \([0,\infty)\).
- b
tuning parameter for within-class weight in \([0,\infty)\).
- lambda
balance parameter for between-class and within-class scatter matrices in \((0,\infty)\).
Value
a named list containing
- Y
an \((n\times ndim)\) matrix whose rows are embedded observations.
- trfinfo
a list containing information for out-of-sample prediction.
- projection
a \((p\times ndim)\) whose columns are basis for projection.
References
Lu J, Tan Y (2011). “Adaptive Maximum Margin Criterion for Image Classification.” In 2011 IEEE International Conference on Multimedia and Expo, 1--6.
See also
Examples
## load iris data
data(iris)
set.seed(100)
subid = sample(1:150,50)
X = as.matrix(iris[subid,1:4])
label = as.factor(iris[subid,5])
## try different lambda values
out1 = do.ammc(X, label, lambda=0.1)
out2 = do.ammc(X, label, lambda=1)
out3 = do.ammc(X, label, lambda=10)
## visualize
opar <- par(no.readonly=TRUE)
par(mfrow=c(1,3))
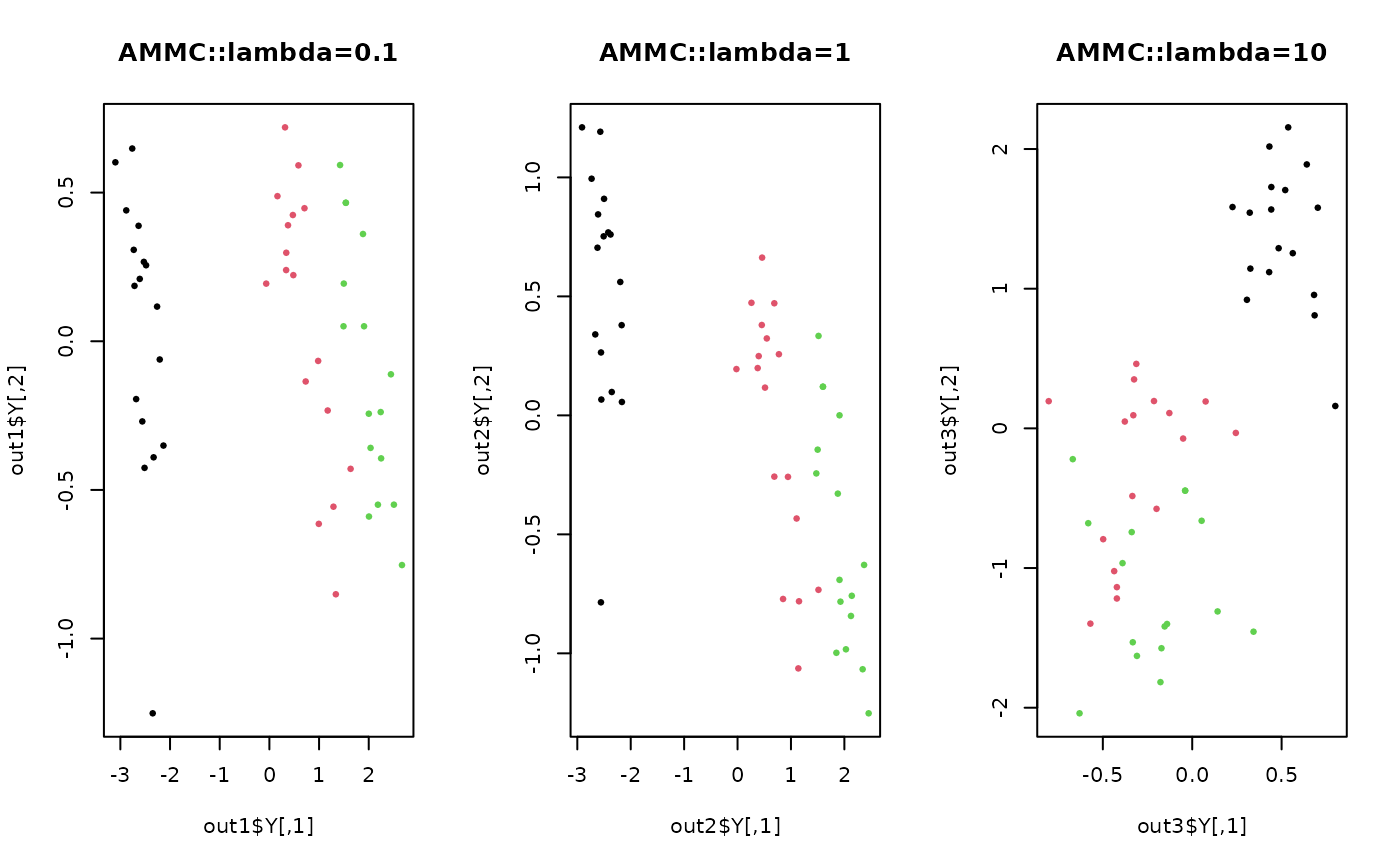
plot(out1$Y, main="AMMC::lambda=0.1", pch=19, cex=0.5, col=label)
plot(out2$Y, main="AMMC::lambda=1", pch=19, cex=0.5, col=label)
plot(out3$Y, main="AMMC::lambda=10", pch=19, cex=0.5, col=label)
 par(opar)
par(opar)