Numerical Approximation to Gradient of a Function with Matrix Argument

For a given function \(f:\mathbf{R}^{n\times p} \rightarrow \mathbf{R}\), we use finite difference scheme that approximates a gradient at a given point \(x\). In Riemannian optimization, this can be used as a proxy for ambient gradient. Use with care since it may accumulate numerical error.

matderiv(fn, x, h = 0.001)

Arguments

fn

a function that takes a matrix of size \((n\times p)\) and returns a scalar value.

x

an \((n\times p)\) matrix where the gradient is to be computed.

h

step size for centered difference scheme.

Value

an approximate numerical gradient matrix of size \((n\times p)\).

References

Kincaid D, Cheney EW (2009). Numerical Analysis: Mathematics of Scientific Computing, number 2 in Pure and Applied Undergraduate Texts, 3. ed edition. American Mathematical Society, Providence, RI.

Examples

## function f(X) = <a,Xb> for two vectors 'a' and 'b'
#  derivative w.r.t X is ab'
#  take an example of (5x5) symmetric positive definite matrix

#  problem settings
a   <- rnorm(5)
b   <- rnorm(5)
ftn <- function(X){
  return(sum(as.vector(X%*%b)*a))
}       # function to be taken derivative
myX <- matrix(rnorm(25),nrow=5)  # point where derivative is evaluated
myX <- myX%*%t(myX)

# main computation
sol.true <- base::outer(a,b)
sol.num1 <- matderiv(ftn, myX, h=1e-1) # step size : 1e-1
sol.num2 <- matderiv(ftn, myX, h=1e-5) #             1e-3
sol.num3 <- matderiv(ftn, myX, h=1e-9) #             1e-5

## visualize/print the results
expar = par(no.readonly=TRUE)
par(mfrow=c(2,2),pty="s")
image(sol.true, main="true solution")
image(sol.num1, main="h=1e-1")
image(sol.num2, main="h=1e-5")
image(sol.num3, main="h=1e-9")

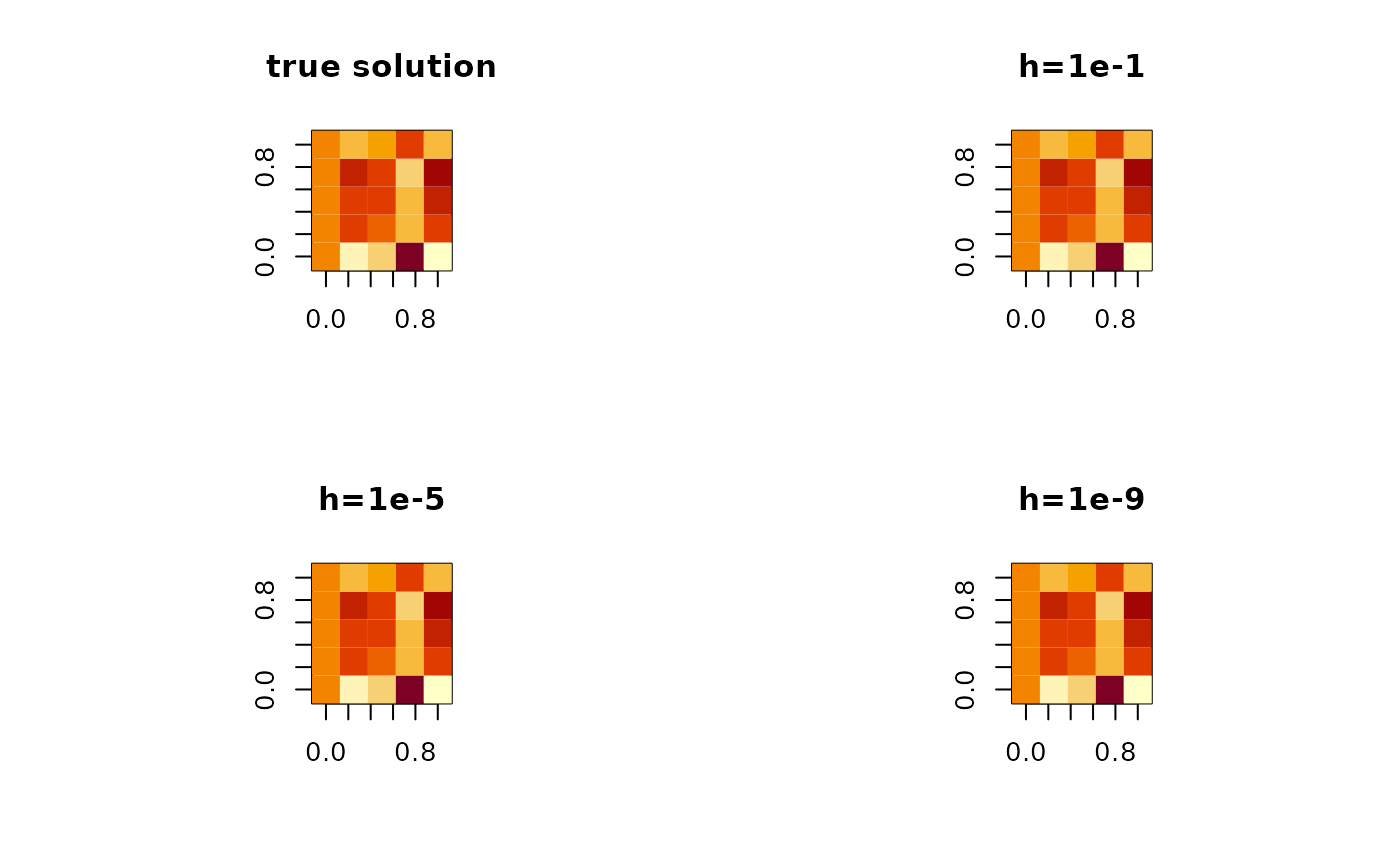par(expar)

# \donttest{
ntrue = norm(sol.true,"f")
cat('* Relative Errors in Frobenius Norm ')
#> * Relative Errors in Frobenius Norm 
cat(paste("*  h=1e-1   : ",norm(sol.true-sol.num1,"f")/ntrue,sep=""))
#> *  h=1e-1   : 2.47435845237516e-15
cat(paste("*  h=1e-5   : ",norm(sol.true-sol.num2,"f")/ntrue,sep=""))
#> *  h=1e-5   : 2.35670523982772e-11
cat(paste("*  h=1e-9   : ",norm(sol.true-sol.num3,"f")/ntrue,sep=""))
#> *  h=1e-9   : 1.97572724360866e-08
# }