Wasserstein Median of Gaussian Distributions in \(\mathbf{R}^p\)

Given a collection of \(p\)-dimensional Gaussian distributions \(\mathcal{N}(\mu_i, \sigma_i^2)\) for \(i=1,\ldots,n\), compute the Wasserstein median.

Usage

gaussmedpd(means, vars, weights = NULL, ...)

Arguments

means

an \((n\times p)\) matrix whose rows are mean vectors.

vars

a \((p\times p\times n)\) array where each slice is covariance matrix.

weights

a weight of each image; if NULL (default), uniform weight is set. Otherwise, it should be a length-\(n\) vector of nonnegative weights.

...

extra parameters including

abstol

stopping criterion for iterations (default: 1e-8).

maxiter

maximum number of iterations (default: 496).

Value

a named list containing

mean

a length-\(p\) vector for mean of the estimated median distribution.

var

a \((p\times p)\) matrix for variance of the estimated median distribution.

See also

gaussmed1d() for univariate case.

Examples

# \donttest{
#----------------------------------------------------------------------
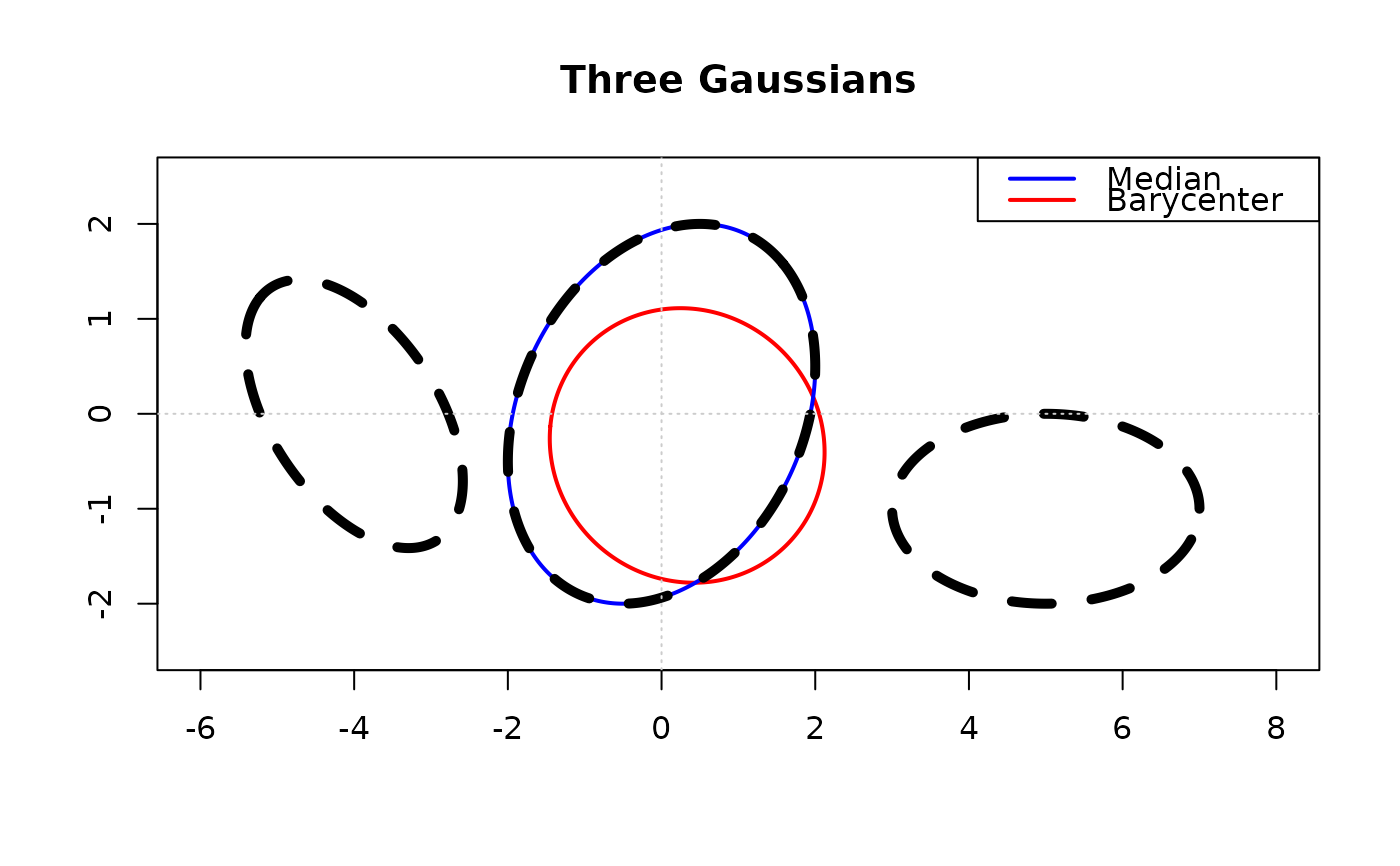
#                         Three Gaussians in R^2
#----------------------------------------------------------------------
# GENERATE PARAMETERS
# means
par_mean = rbind(c(-4,0), c(0,0), c(5,-1))

# covariances
par_vars = array(0,c(2,2,3))
par_vars[,,1] = cbind(c(2,-1),c(-1,2))
par_vars[,,2] = cbind(c(4,+1),c(+1,4))
par_vars[,,3] = diag(c(4,1))

# COMPUTE THE MEDIAN
gmeds = gaussmedpd(par_mean, par_vars)

# COMPUTE THE BARYCENTER 
gmean = gaussbarypd(par_mean, par_vars)

# GET COORDINATES FOR DRAWING
pt_type1 = gaussvis2d(par_mean[1,], par_vars[,,1])
pt_type2 = gaussvis2d(par_mean[2,], par_vars[,,2])
pt_type3 = gaussvis2d(par_mean[3,], par_vars[,,3])
pt_gmean = gaussvis2d(gmean$mean, gmean$var)
pt_gmeds = gaussvis2d(gmeds$mean, gmeds$var)

# VISUALIZE
opar <- par(no.readonly=TRUE)
plot(pt_gmean, lwd=2, col="red", type="l",
     main="Three Gaussians", xlab="", ylab="", 
     xlim=c(-6,8), ylim=c(-2.5,2.5))
lines(pt_gmeds, lwd=2, col="blue")
lines(pt_type1, lty=2, lwd=5)
lines(pt_type2, lty=2, lwd=5)
lines(pt_type3, lty=2, lwd=5)
abline(h=0, col="grey80", lty=3)
abline(v=0, col="grey80", lty=3)
legend("topright", legend=c("Median","Barycenter"),
       lwd=2, lty=1, col=c("blue","red"))

par(opar)
# }