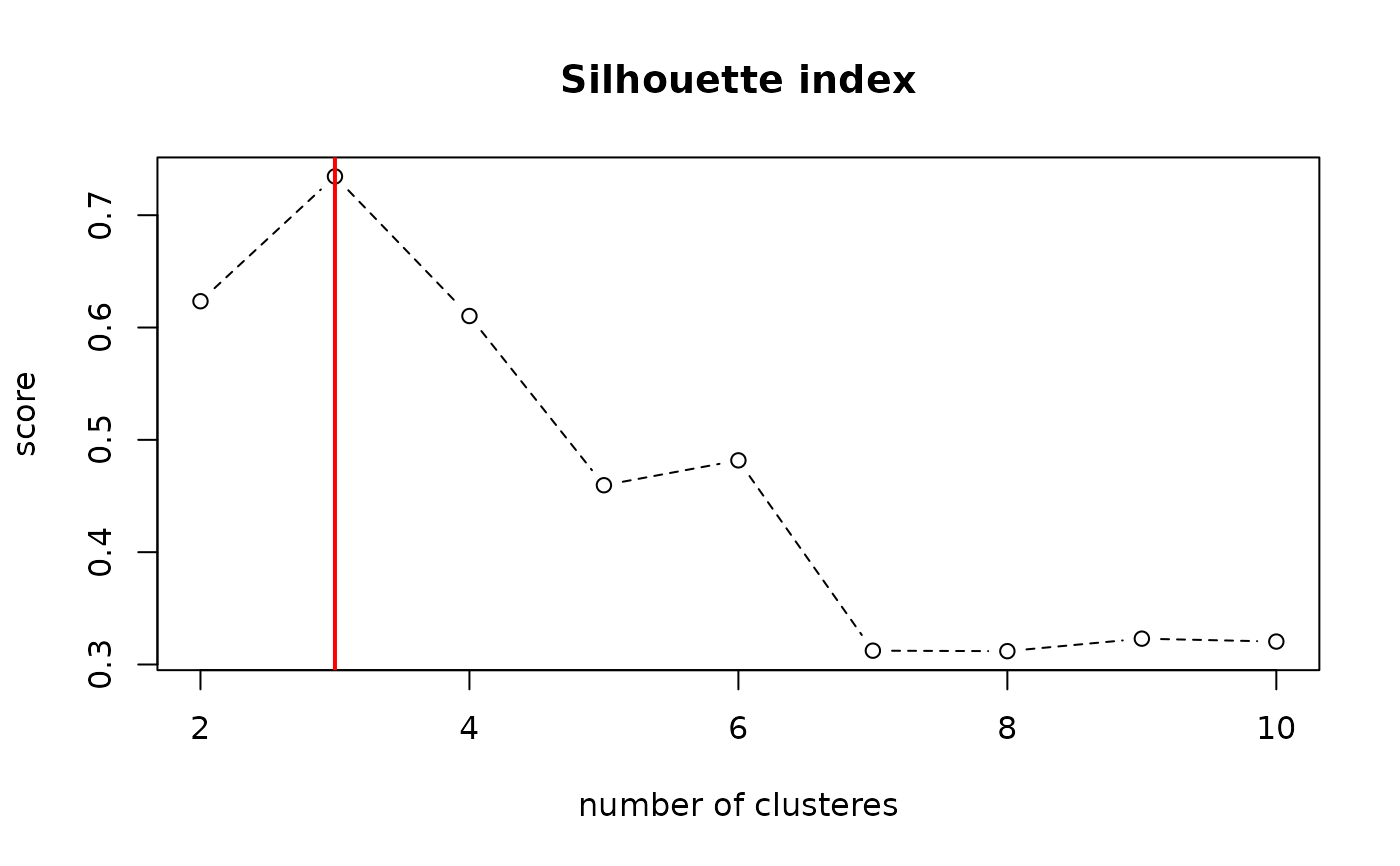
(+) Silhouette Index

Silhouette index in \([0,1]\). Higher score means a good clustering.

quality.sil(data, cluster)

Arguments

data	an \((n\times p)\) matrix of row-stacked observations, or dist object.
cluster	a length-\(n\) vector of class labels (from \(1:k\)).

Value

an index value.

Examples

# \donttest{
# -------------------------------------------------------------
#        clustering validity check with 3 Gaussians
# -------------------------------------------------------------
## PREPARE
X1 = matrix(rnorm(30*3, mean=-5), ncol=3)
X2 = matrix(rnorm(30*3), ncol=3)
X3 = matrix(rnorm(30*3, mean=5), ncol=3)
XX = rbind(X1, X2, X3)

## CLUSTERING WITH DIFFERENT K VALUES & COMPUTE QUALITY INDICES
vec_k  = 2:10
vec_cl = rep(0, 9)
for (i in 1:length(vec_k)){
  cl_now    = T4cluster::kmeans(XX, k=vec_k[i])$cluster
  vec_cl[i] = quality.sil(XX, cl_now)
}


## VISUALIZE
opar <- par(no.readonly=TRUE)
plot(vec_k, vec_cl, type="b", lty=2, xlab="number of clusteres",
     ylab="score", main="Silhouette index")
abline(v=3, lwd=2, col="red")
par(opar)
# }