The simplest way of out-of-sample extension might be linear regression even though the original embedding is not the linear type by solving $$\textrm{min}_{\beta} \|X_{old} \beta - Y_{old}\|_2^2$$ and use the estimate \(\hat{beta}\) to acquire $$Y_{new} = X_{new} \hat{\beta}$$.
oos.linproj(Xold, Yold, Xnew)Arguments
- Xold
an \((n\times p)\) matrix of data in original high-dimensional space.
- Yold
an \((n\times ndim)\) matrix of data in reduced-dimensional space.
- Xnew
an \((m\times p)\) matrix for out-of-sample extension.
Value
an \((m\times ndim)\) matrix whose rows are embedded observations.
Examples
# \donttest{
## generate sample data and separate them
data(iris, package="Rdimtools")
X = as.matrix(iris[,1:4])
lab = as.factor(as.vector(iris[,5]))
ids = sample(1:150, 30)
Xold = X[setdiff(1:150,ids),] # 80% of data for training
Xnew = X[ids,] # 20% of data for testing
## run PCA for train data & use the info for prediction
training = do.pca(Xold,ndim=2)
Yold = training$Y
Ynew = Xnew%*%training$projection
Yplab = lab[ids]
## perform out-of-sample prediction
Yoos = oos.linproj(Xold, Yold, Xnew)
## visualize
opar <- par(no.readonly=TRUE)
par(mfrow=c(1,2))
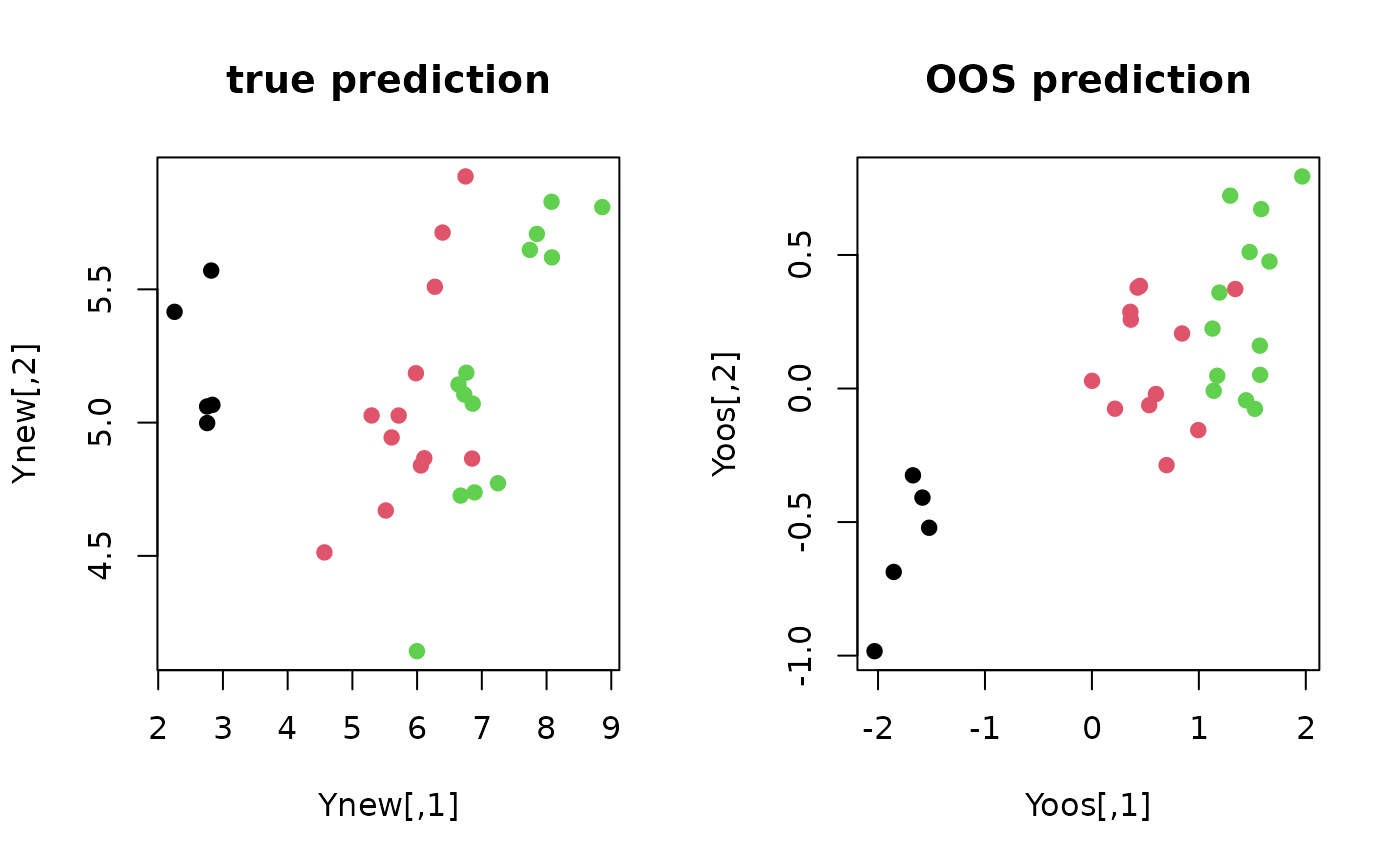
plot(Ynew, pch=19, col=Yplab, main="true prediction")
plot(Yoos, pch=19, col=Yplab, main="OOS prediction")
 par(opar)
# }
par(opar)
# }