Robust Euclidean Embedding

Robust Euclidean Embedding (REE) is an embedding procedure exploiting robustness of \(\ell_1\) cost function. In our implementation, we adopted a generalized version with weight matrix to be applied as well. Its original paper introduced a subgradient algorithm to overcome memory-intensive nature of original semidefinite programming formulation.

do.ree(
  X,
  ndim = 2,
  W = NA,
  preprocess = c("null", "center", "scale", "cscale", "whiten", "decorrelate"),
  initc = 1,
  dmethod = c("euclidean", "maximum", "manhattan", "canberra", "binary", "minkowski"),
  maxiter = 100,
  abstol = 0.001
)

Arguments

X

an \((n\times p)\) matrix or data frame whose rows are observations and columns represent independent variables.

ndim

an integer-valued target dimension.

W

an \((n\times n)\) weight matrix. Default is uniform weight of 1s.

preprocess

an additional option for preprocessing the data. Default is "null". See also aux.preprocess for more details.

initc

initial c value for subgradient iterating stepsize, \(c/\sqrt{i}\).

dmethod

a type of distance measure. See dist for more details.

maxiter

maximum number of iterations for subgradient descent method.

abstol

stopping criterion for subgradient descent method.

Value

a named list containing

Y

an \((n\times ndim)\) matrix whose rows are embedded observations.

niter

the number of iterations taken til convergence.

trfinfo

a list containing information for out-of-sample prediction.

References

Cayton L, Dasgupta S (2006). “Robust Euclidean Embedding.” In Proceedings of the 23rd International Conference on Machine Learning, ICML '06, 169--176.

Author

Kisung You

Examples

# \donttest{
## use iris data
data(iris)
set.seed(100)
subid = sample(1:150,50)
X     = as.matrix(iris[subid,1:4])
label = as.factor(iris[subid,5])

## try different distance method
output1 <- do.ree(X, maxiter=50, dmethod="euclidean")
output2 <- do.ree(X, maxiter=50, dmethod="maximum")
output3 <- do.ree(X, maxiter=50, dmethod="canberra")

## visualize three different projections
opar <- par(no.readonly=TRUE)
par(mfrow=c(1,3))
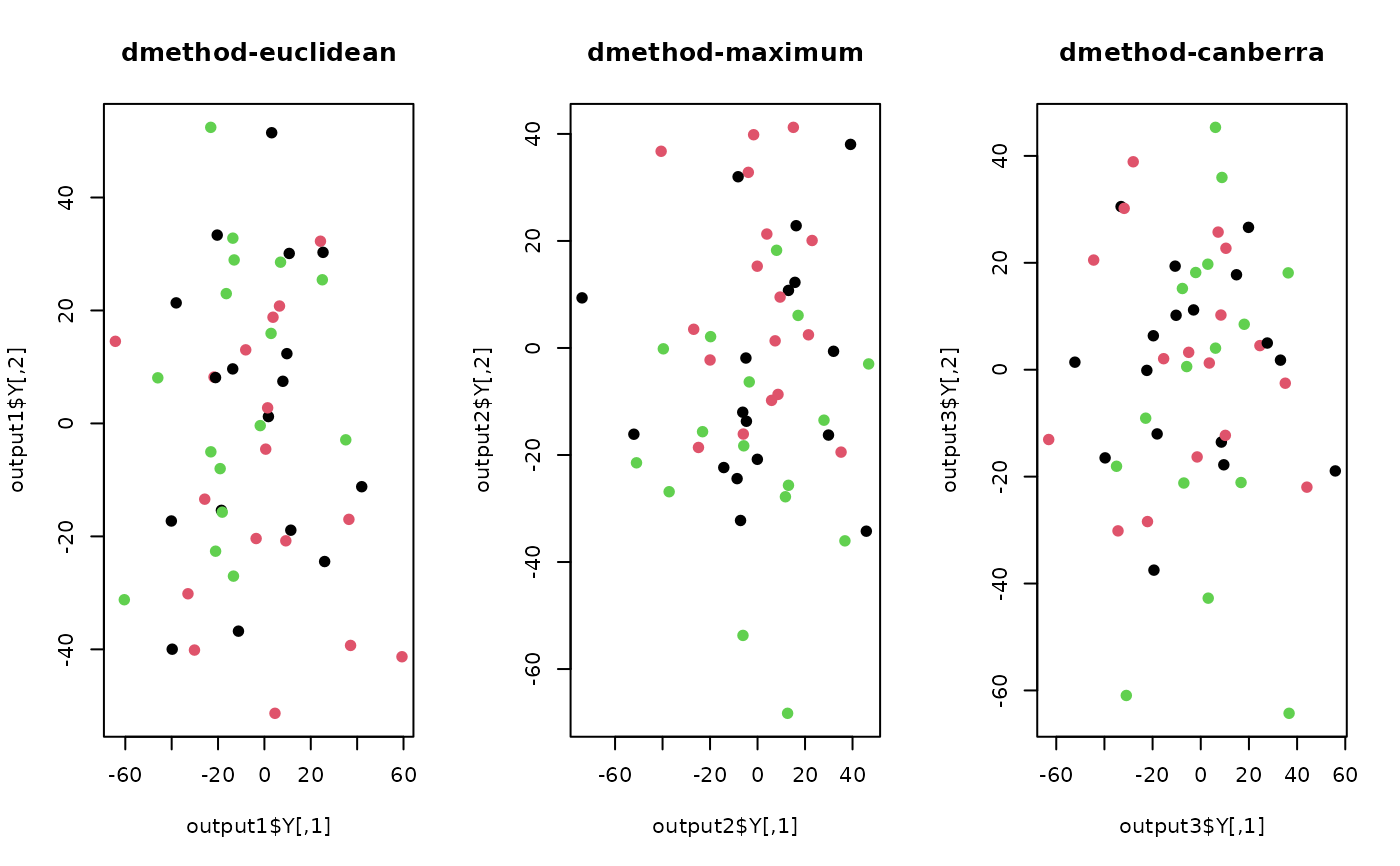
plot(output1$Y, col=label, pch=19, main="dmethod-euclidean")
plot(output2$Y, col=label, pch=19, main="dmethod-maximum")
plot(output3$Y, col=label, pch=19, main="dmethod-canberra")

par(opar)
# }