Hyperbolic Distance Recovery and Approximation

Source: R/nonlinear_HYDRA.R

Hyperbolic Distance Recovery and Approximation, also known as hydra in short, implements embedding of distance-based data into hyperbolic space represented as the Poincare disk, which is interior of a hypersphere.

do.hydra(X, ndim = 2, ...)

Arguments

X

an \((n\times p)\) matrix or data frame whose rows are observations and columns represent independent variables.

ndim

an integer-valued target dimension (default: 2).

...

extra parameters including

kappa

embedding curvature, which is a nonnegative number (default: 1).

iso.adjust

perform isotropic adjustment. If ndim=2, default is FALSE. Otherwise, TRUE is used as default.

Value

a named Rdimtools S3 object containing

Y

an \((n\times ndim)\) matrix whose rows are embedded observations in the Poincare disk.

algorithm

name of the algorithm.

References

Keller-Ressel M, Nargang S (2020). “Hydra: A Method for Strain-Minimizing Hyperbolic Embedding of Network- and Distance-Based Data.” Journal of Complex Networks, 8(1), cnaa002. ISSN 2051-1329.

Examples

# \donttest{
## load iris data
data(iris)
X     = as.matrix(iris[,1:4])
lab   = as.factor(iris[,5])

## multiple runs with varying curvatures
embed1 <- do.hydra(X, kappa=0.1)
embed2 <- do.hydra(X, kappa=1)
embed3 <- do.hydra(X, kappa=10)

## Visualize
opar <- par(no.readonly=TRUE)
par(mfrow=c(1,3), pty="s")
plot(embed1$Y , col=lab, pch=19, main="kappa=0.1")
plot(embed2$Y , col=lab, pch=19, main="kappa=1")
plot(embed3$Y , col=lab, pch=19, main="kappa=10")

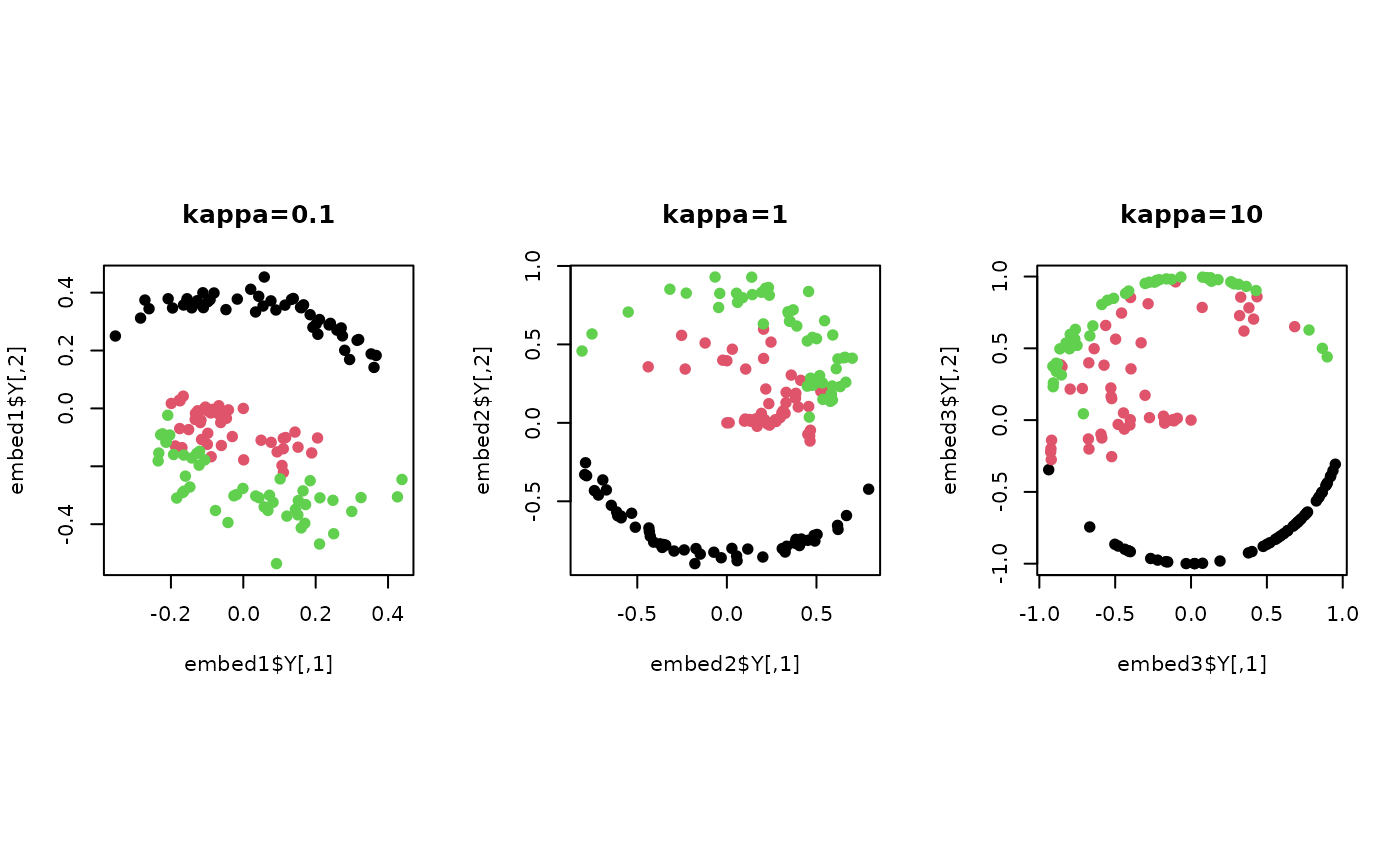par(opar)
# }