Independent Component Analysis

do.ica is an R implementation of FastICA algorithm, which aims at finding weight vectors that maximize a measure of non-Gaussianity of projected data. FastICA is initiated with pre-whitening of the data. Single and multiple component extraction are both supported. For more detailed information on ICA and FastICA algorithm, see this Wikipedia page.

do.ica(
  X,
  ndim = 2,
  type = "logcosh",
  tpar = 1,
  sym = FALSE,
  tol = 1e-06,
  redundancy = TRUE,
  maxiter = 100
)

Arguments

X

an \((n\times p)\) matrix or data frame whose rows are observations and columns represent independent variables.

ndim

an integer-valued target dimension.

type

nonquadratic function, one of "logcosh","exp", or "poly" be chosen.

tpar

a numeric parameter for logcosh and exp parameters that should be close to 1.

sym

a logical value; FALSE for not using symmetric decorrelation, TRUE otherwise.

tol

stopping criterion for iterative update.

redundancy

a logical value; TRUE for removing NA values after prewhitening, FALSE otherwise.

maxiter

maximum number of iterations allowed.

Y

an \((n\times ndim)\) matrix whose rows are embedded observations.

trfinfo

a list containing information for out-of-sample prediction.

projection

a \((p\times ndim)\) whose columns are basis for projection.

Details

In most of ICA literature, we have $$S = X*W$$ where \(W\) is an unmixing matrix for the given data \(X\). In order to preserve consistency throughout our package, we changed the notation; \(Y\) a projected matrix for \(S\), and projection for unmixing matrix \(W\).

References

Hyvarinen A, Karhunen J, Oja E (2001). Independent Component Analysis. J. Wiley, New York. ISBN 978-0-471-40540-5.

Author

Kisung You

Examples

## use iris dataset
data(iris)
set.seed(100)
subid = sample(1:150,50)
X     = as.matrix(iris[subid,1:4])
lab   = as.factor(iris[subid,5])

## 1. use logcosh function for transformation
output1 <- do.ica(X,ndim=2,type="logcosh")

## 2. use exponential function for transformation
output2 <- do.ica(X,ndim=2,type="exp")

## 3. use polynomial function for transformation
output3 <- do.ica(X,ndim=2,type="poly")

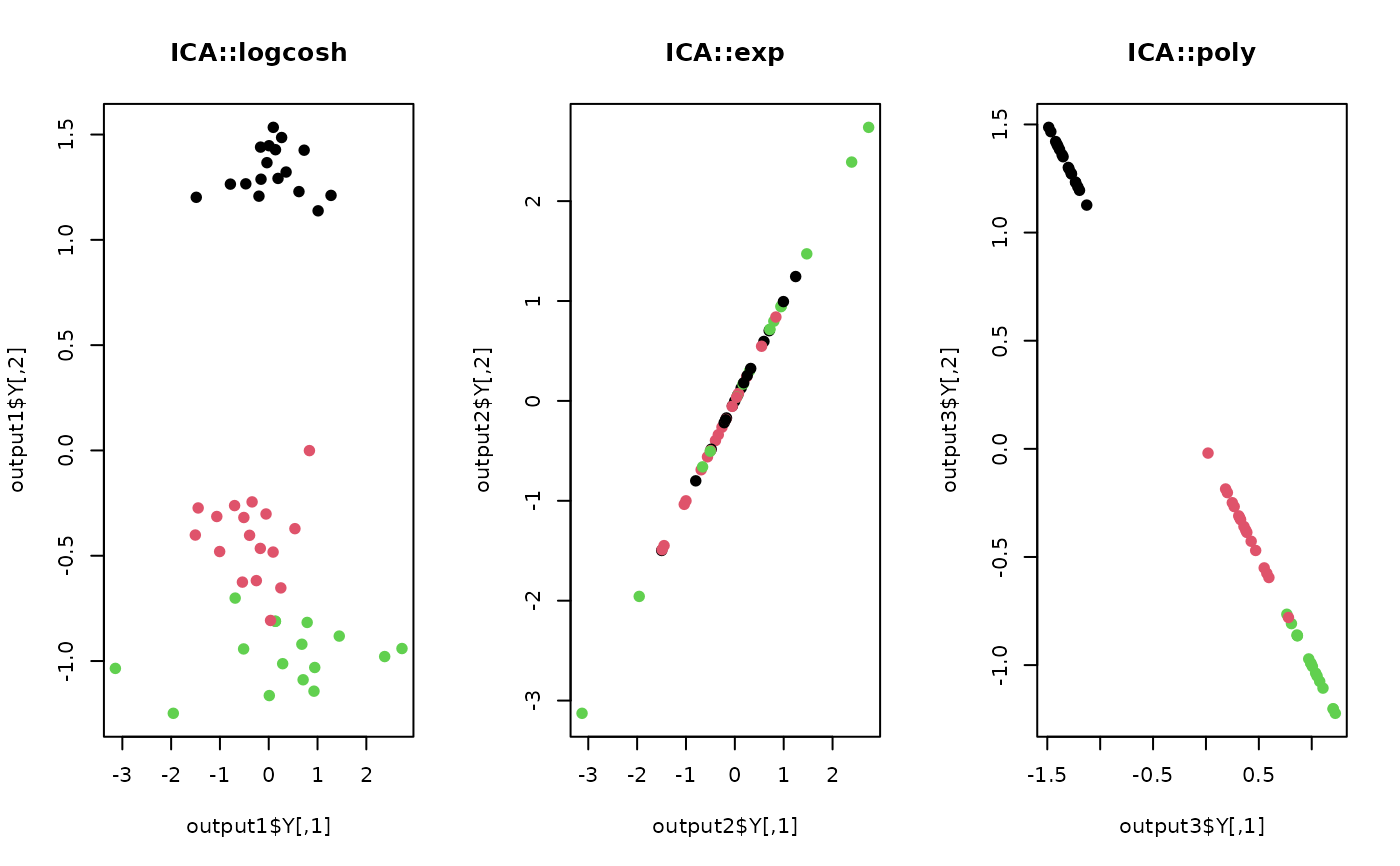
## Visualize three different projections
opar <- par(no.readonly=TRUE)
par(mfrow=c(1,3))
plot(output1$Y, col=lab, pch=19, main="ICA::logcosh")
plot(output2$Y, col=lab, pch=19, main="ICA::exp")
plot(output3$Y, col=lab, pch=19, main="ICA::poly")

par(opar)