do.fa is an optimization-based implementation of a popular technique for Exploratory Data Analysis.
It is closely related to principal component analysis.
do.fa(X, ndim = 2, ...)Arguments
- X
an \((n\times p)\) matrix whose rows are observations and columns represent independent variables.
- ndim
an integer-valued number of loading variables, or target dimension.
- ...
extra parameters including
- maxiter
maximum number of iterations (default: 10).
- tolerance
stopping criterion in a Frobenius norm (default: 1e-8).
Value
a named Rdimtools S3 object containing
- Y
an \((n\times ndim)\) matrix whose rows are embedded observations.
- projection
a \((p\times ndim)\) whose columns are basis for projection.
- loadings
a \((p\times ndim)\) matrix whose rows are extracted loading factors.
- noise
a length-\(p\) vector of estimated noise.
- algorithm
name of the algorithm.
References
Spearman C (1904). “"General Intelligence," Objectively Determined and Measured.” The American Journal of Psychology, 15(2), 201.
Examples
# \donttest{
## use iris data
data(iris)
set.seed(100)
subid = sample(1:150,50)
X = as.matrix(iris[subid,1:4])
lab = as.factor(iris[subid,5])
## compare with PCA and MDS
out1 <- do.fa(X, ndim=2)
out2 <- do.mds(X, ndim=2)
out3 <- do.pca(X, ndim=2)
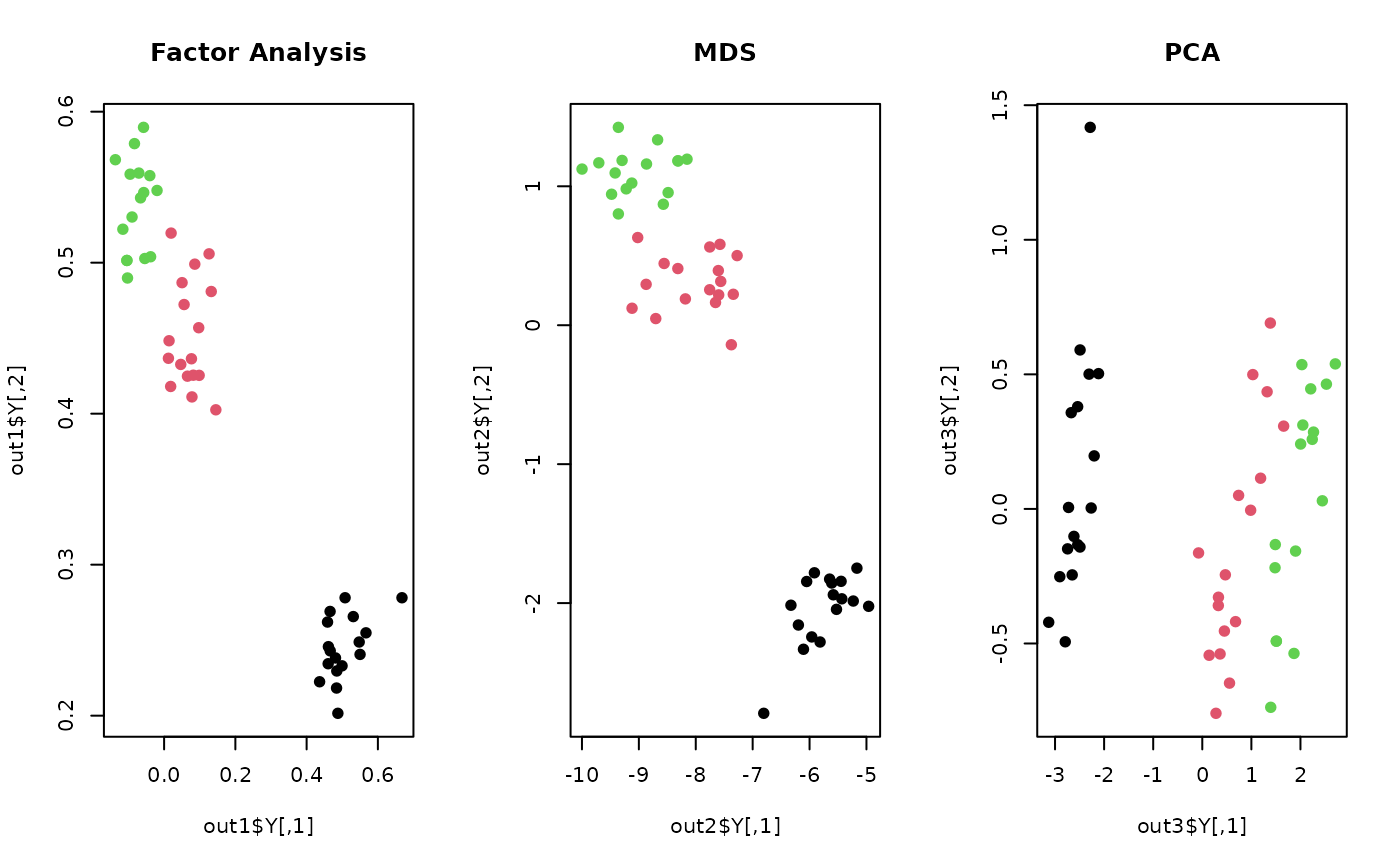
## visualize three different projections
opar <- par(no.readonly=TRUE)
par(mfrow=c(1,3))
plot(out1$Y, pch=19, col=lab, main="Factor Analysis")
plot(out2$Y, pch=19, col=lab, main="MDS")
plot(out3$Y, pch=19, col=lab, main="PCA")
 par(opar)
# }
par(opar)
# }