Feature Selection using PCA and Procrustes Analysis

do.procrustes selects a set of features that best aligns PCA's coordinates in the embedded low dimension. It iteratively selects each variable that minimizes Procrustes distance between configurations.

do.procrustes(X, ndim = 2, intdim = (ndim - 1), cor = TRUE)

Arguments

X

an \((n\times p)\) matrix whose rows are observations and columns represent independent variables.

ndim

an integer-valued target dimension.

intdim

intrinsic dimension of PCA to be applied. It should be smaller than ndim.

cor

mode of eigendecomposition. FALSE for decomposing covariance, and TRUE for correlation matrix in PCA.

Value

a named Rdimtools S3 object containing

Y

an \((n\times ndim)\) matrix whose rows are embedded observations.

featidx

a length-\(ndim\) vector of indices with highest scores.

projection

a \((p\times ndim)\) whose columns are basis for projection.

algorithm

name of the algorithm.

References

Krzanowski WJ (1987). “Selection of Variables to Preserve Multivariate Data Structure, Using Principal Components.” Applied Statistics, 36(1), 22. ISSN 00359254.

Author

Kisung You

Examples

# \donttest{
## use iris data
## it is known that feature 3 and 4 are more important.
data(iris)
iris.dat = as.matrix(iris[,1:4])
iris.lab = as.factor(iris[,5])

## try different strategy
out1 = do.procrustes(iris.dat, cor=TRUE)
out2 = do.procrustes(iris.dat, cor=FALSE)
out3 = do.mifs(iris.dat, iris.lab, beta=0)

## visualize
opar <- par(no.readonly=TRUE)
par(mfrow=c(1, 3))
plot(out1$Y, pch=19, col=iris.lab, main="PCA with Covariance")
plot(out2$Y, pch=19, col=iris.lab, main="PCA with Correlation")
plot(out3$Y, pch=19, col=iris.lab, main="MIFS")

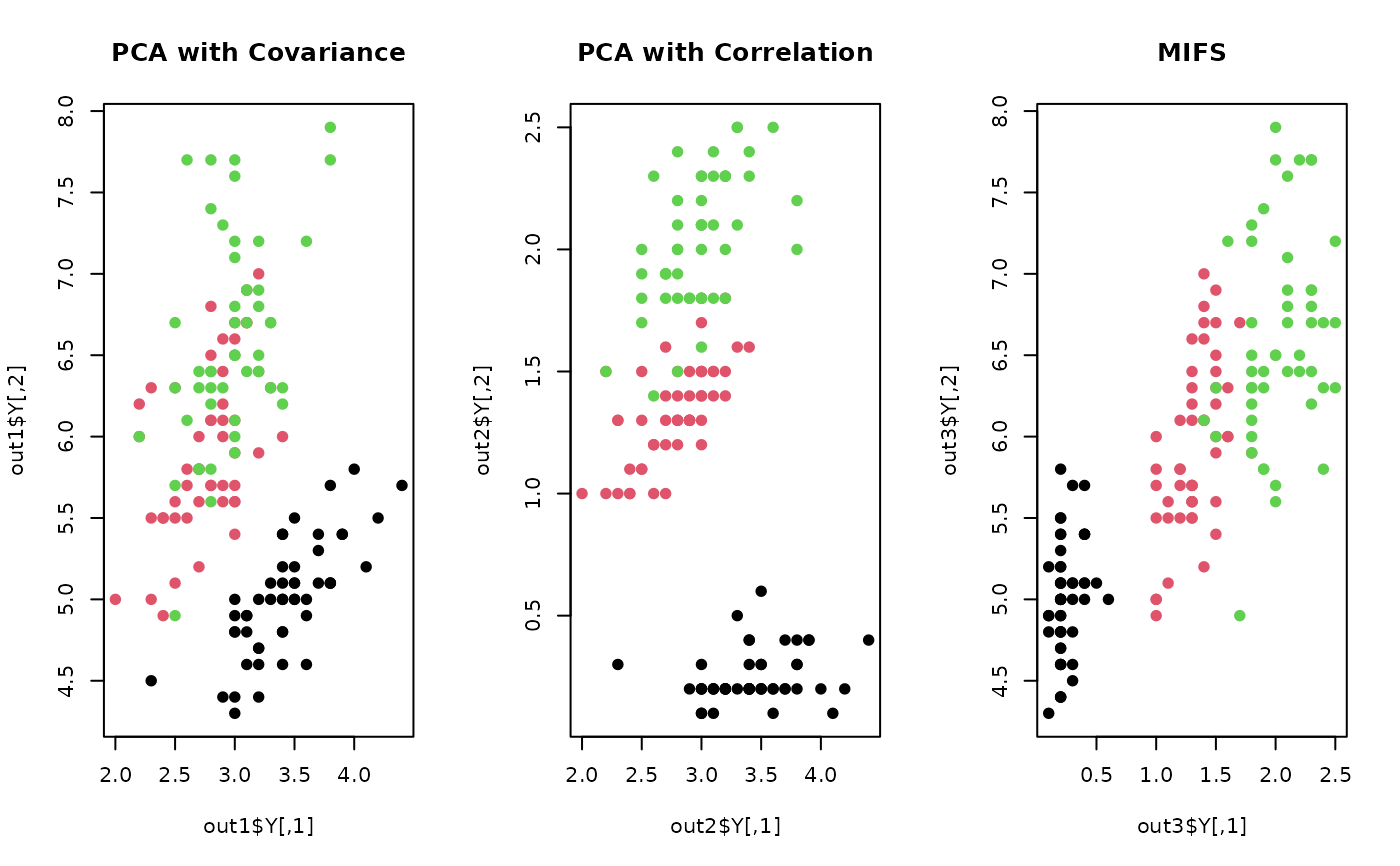par(opar)
# }