Elastic Net is a regularized regression method by solving
$$\textrm{min}_{\beta} ~ \frac{1}{2}\|X\beta-y\|_2^2 + \lambda_1 \|\beta \|_1 + \lambda_2 \|\beta \|_2^2$$
where \(y\) iis response variable in our method. The method can be used in feature selection like LASSO.
do.enet(X, response, ndim = 2, lambda1 = 1, lambda2 = 1)Arguments
- X
an \((n\times p)\) matrix or data frame whose rows are observations and columns represent independent variables.
- response
a length-\(n\) vector of response variable.
- ndim
an integer-valued target dimension.
- lambda1
\(\ell_1\) regularization parameter in \((0,\infty)\).
- lambda2
\(\ell_2\) regularization parameter in \((0,\infty)\).
Value
a named Rdimtools S3 object containing
- Y
an \((n\times ndim)\) matrix whose rows are embedded observations.
- featidx
a length-\(ndim\) vector of indices with highest scores.
- projection
a \((p\times ndim)\) whose columns are basis for projection.
- algorithm
name of the algorithm.
References
Zou H, Hastie T (2005). “Regularization and Variable Selection via the Elastic Net.” Journal of the Royal Statistical Society: Series B (Statistical Methodology), 67(2), 301--320.
Examples
# \donttest{
## generate swiss roll with auxiliary dimensions
## it follows reference example from LSIR paper.
set.seed(100)
n = 123
theta = runif(n)
h = runif(n)
t = (1+2*theta)*(3*pi/2)
X = array(0,c(n,10))
X[,1] = t*cos(t)
X[,2] = 21*h
X[,3] = t*sin(t)
X[,4:10] = matrix(runif(7*n), nrow=n)
## corresponding response vector
y = sin(5*pi*theta)+(runif(n)*sqrt(0.1))
## try different regularization parameters
out1 = do.enet(X, y, lambda1=0.01)
out2 = do.enet(X, y, lambda1=1)
out3 = do.enet(X, y, lambda1=100)
## extract embeddings
Y1 = out1$Y; Y2 = out2$Y; Y3 = out3$Y
## visualize
opar <- par(no.readonly=TRUE)
par(mfrow=c(1,3))
plot(Y1, pch=19, main="ENET::lambda1=0.01")
plot(Y2, pch=19, main="ENET::lambda1=1")
plot(Y3, pch=19, main="ENET::lambda1=100")
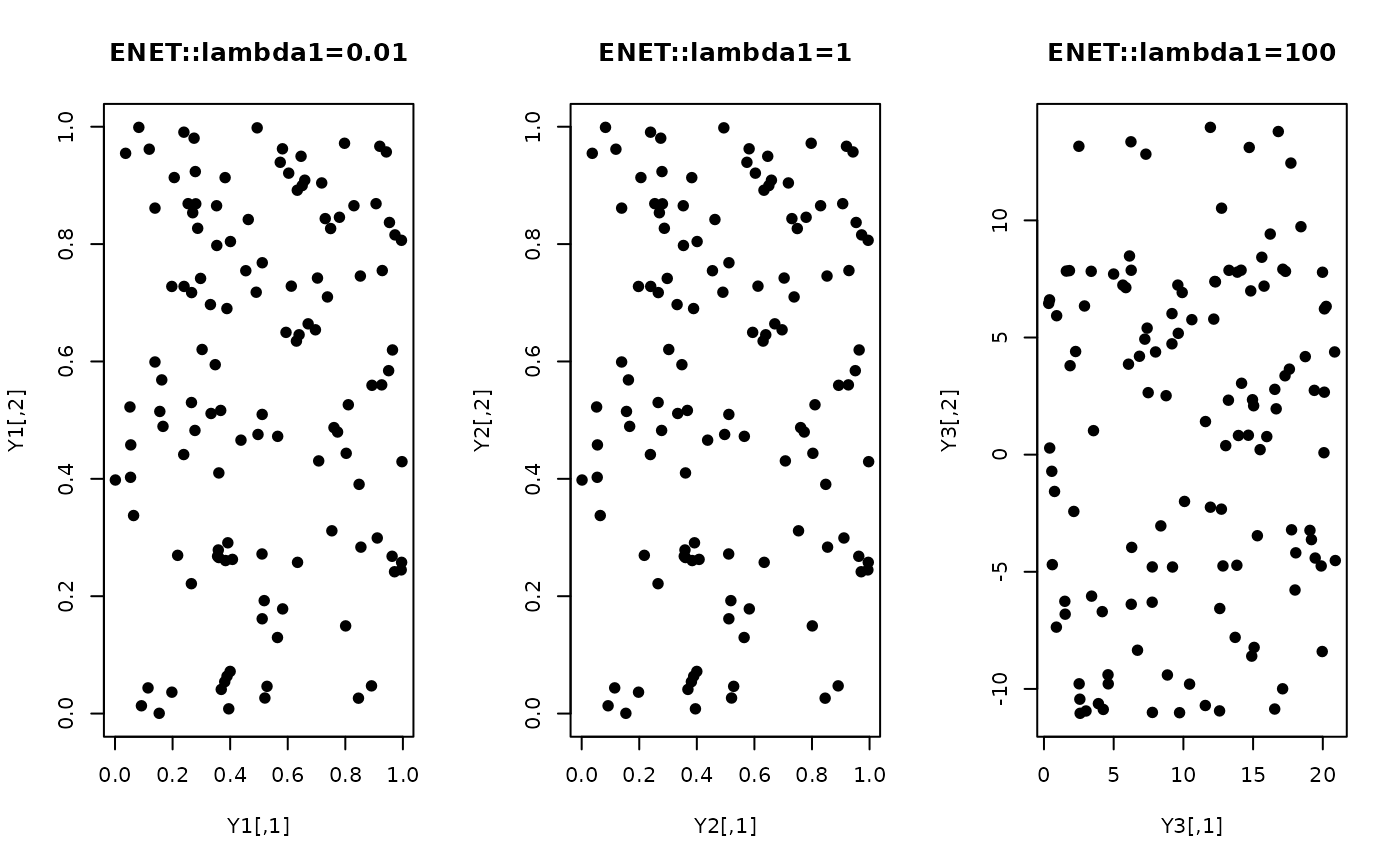 par(opar)
# }
par(opar)
# }